CS224W-Machine Learning with Graph-Graph Transformers

Transformers

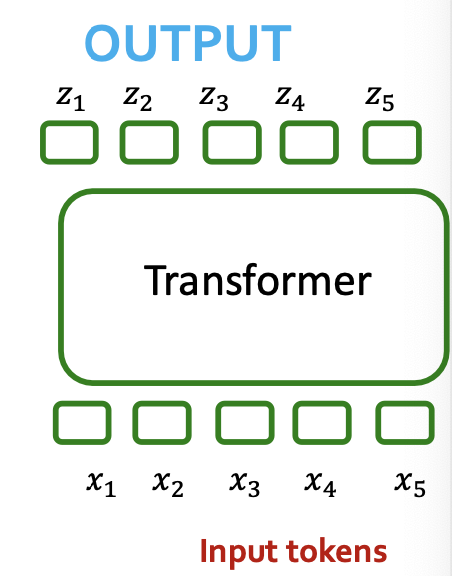
Transformers Ingest Tokens

Transformers map 1D sequences of vectors to 1D sequences of vectors know as tokens
- Tokens describe a “piece” of data - e.g., a word

What output sequence?
- Option 1: next token ⇒ GPT
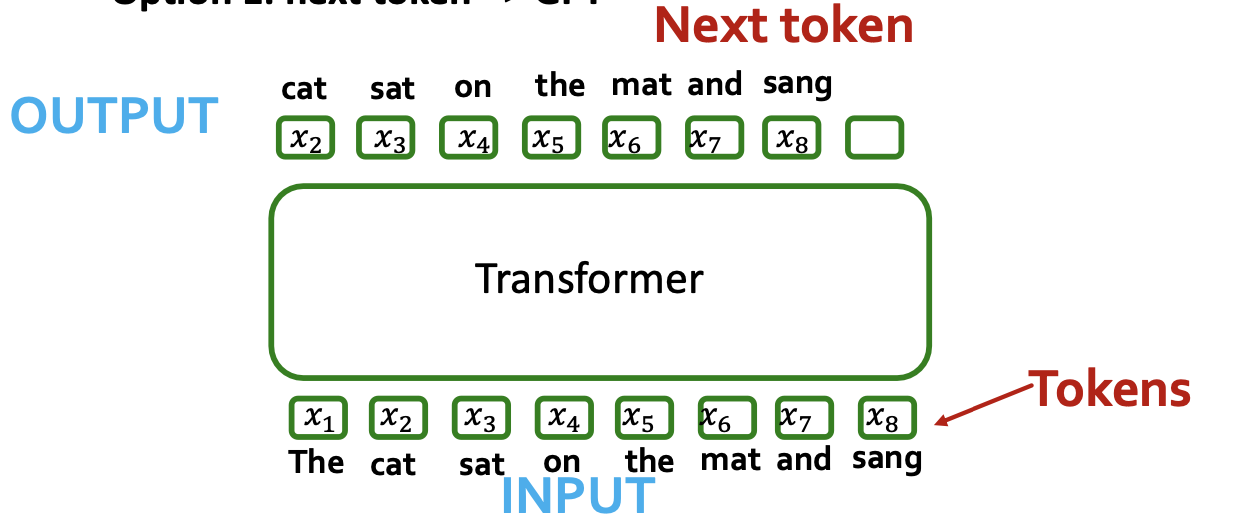
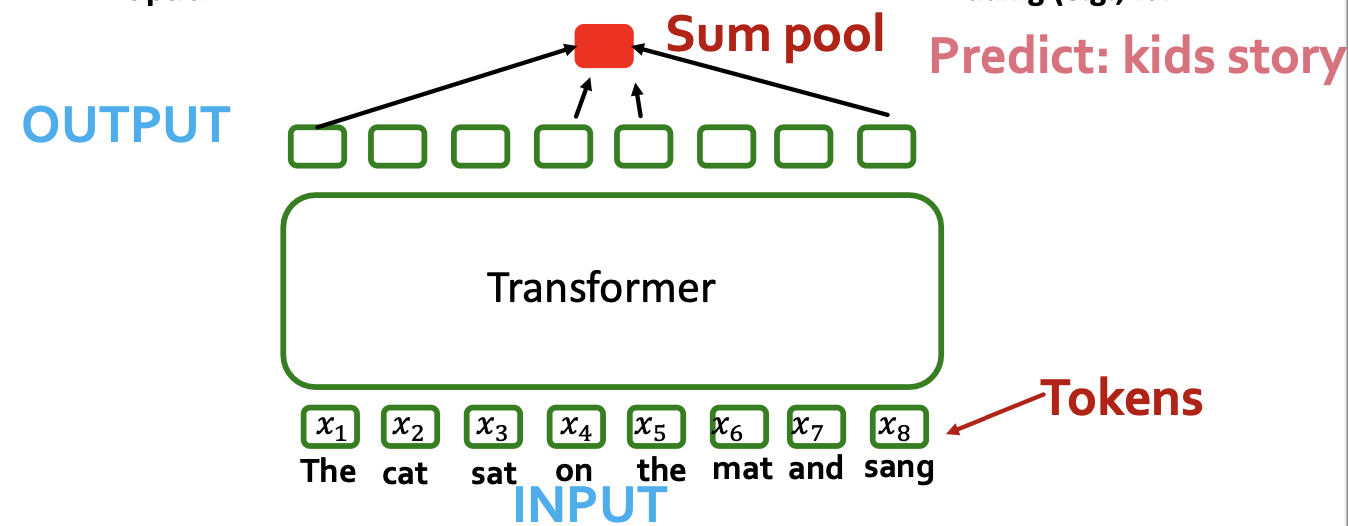
- Option 2: pool (e.g., sum-pool) to get sequence level-embedding (e.g., for classification task)

Transformer Blueprint

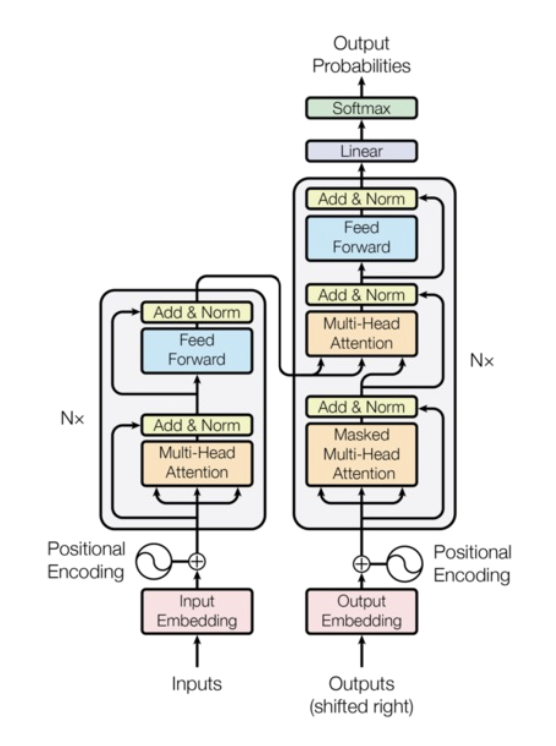
How are tokens processed?

Lots of components
- Normalization
- Feed forward networks
- Positional encoding (more later)
- Multi-head self-attention

What does self-attention block do?

Self-attention

What is “single head” self-attention?

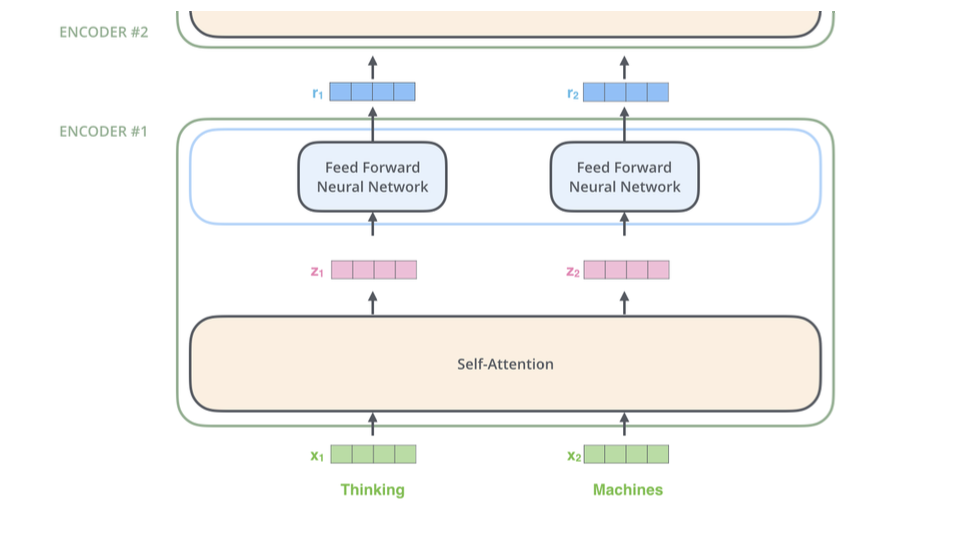
Step 1: compute “key, value, query” for each input

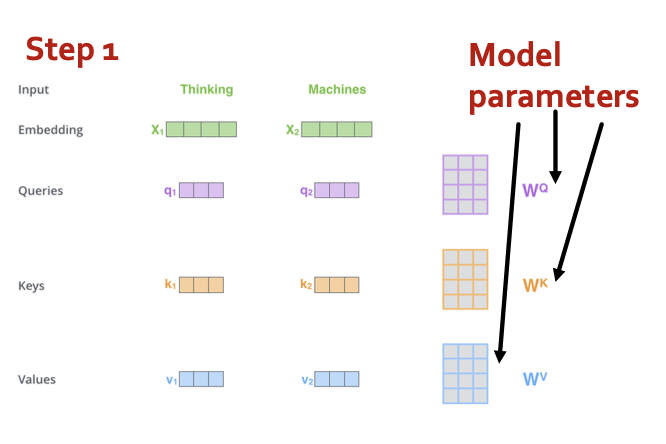
Step 2: (just for $x_1$ ) compute scores between pairs, turn into probabilities (same for $x_2$ ).

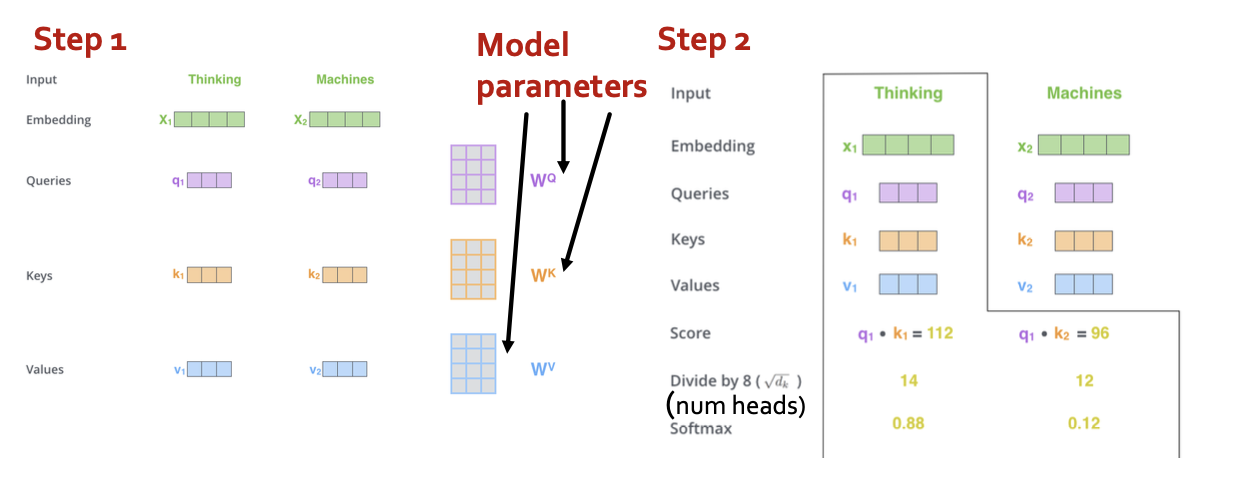
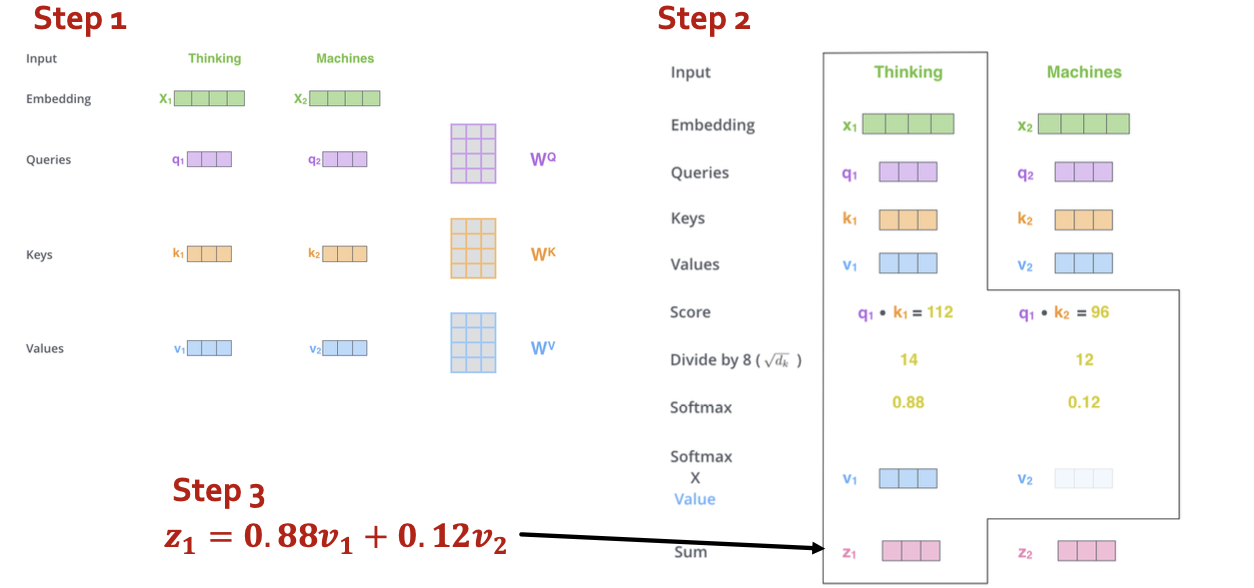
Step 3: get new embedding $z_1$ by weighted sum of $v_1,v_2$

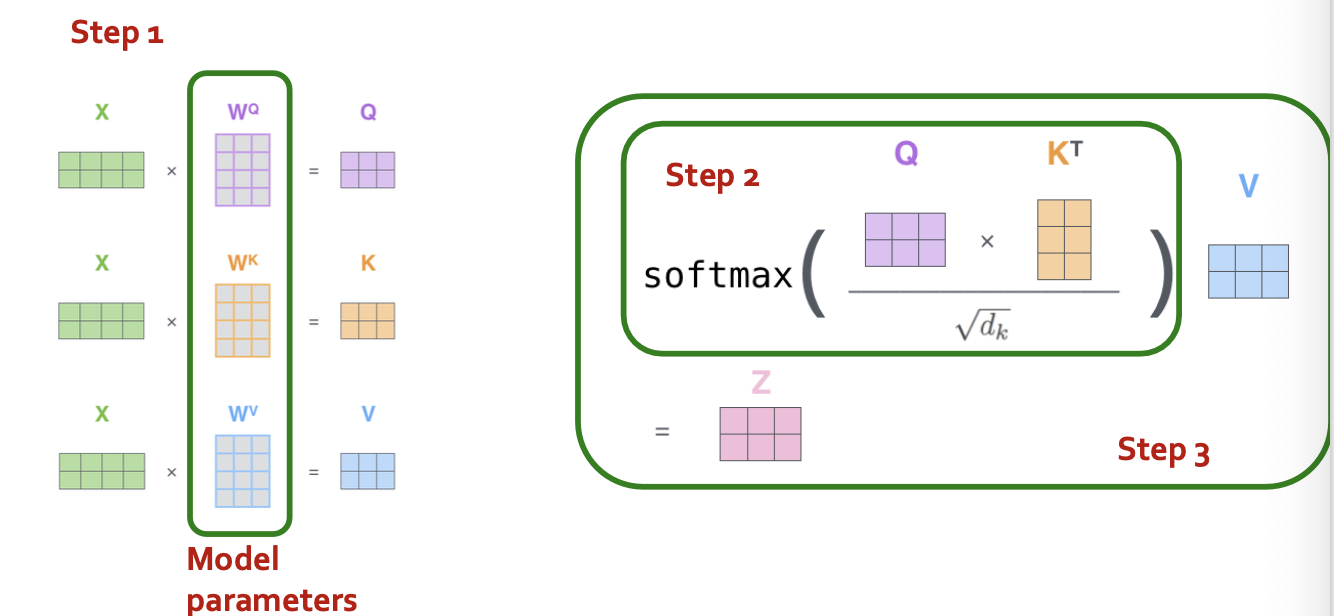
Same calculation in matrix form

Multi-head self-attention

Do many self-attentions in parallel, and combine

Different heads can learn different “similarities” between inputs

Each has own set of parameters

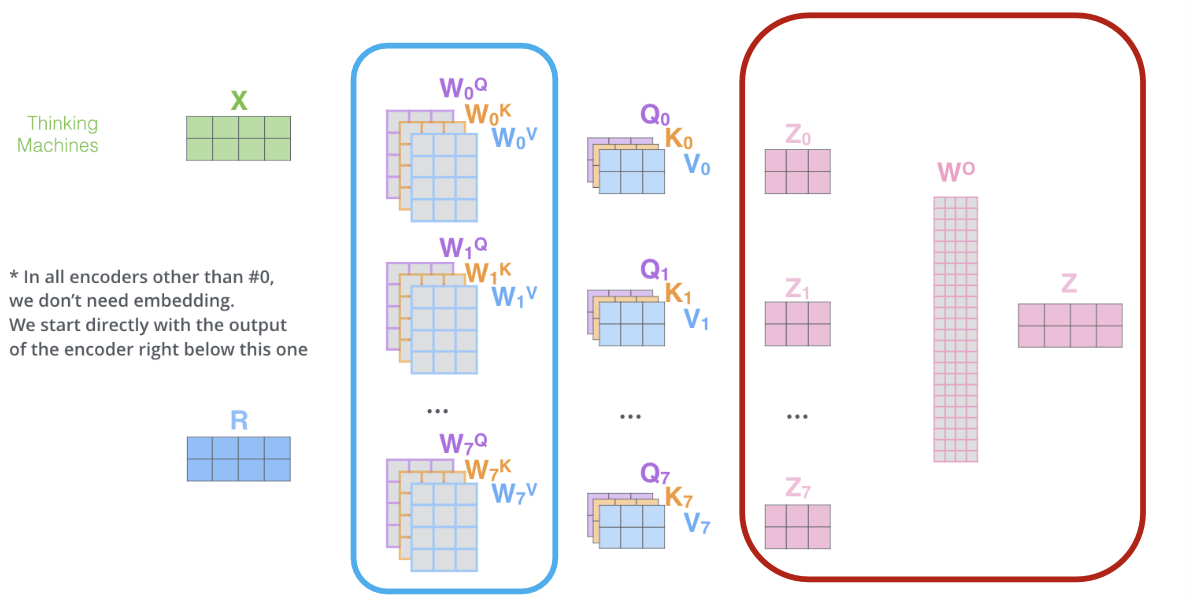
Comparing Transformers and GNN

Similarity: GNNs also take in a sequence of vectors(in no particular order) and output a sequence of embeddings

Difference: GNN use message passing, Transformer uses self-attention

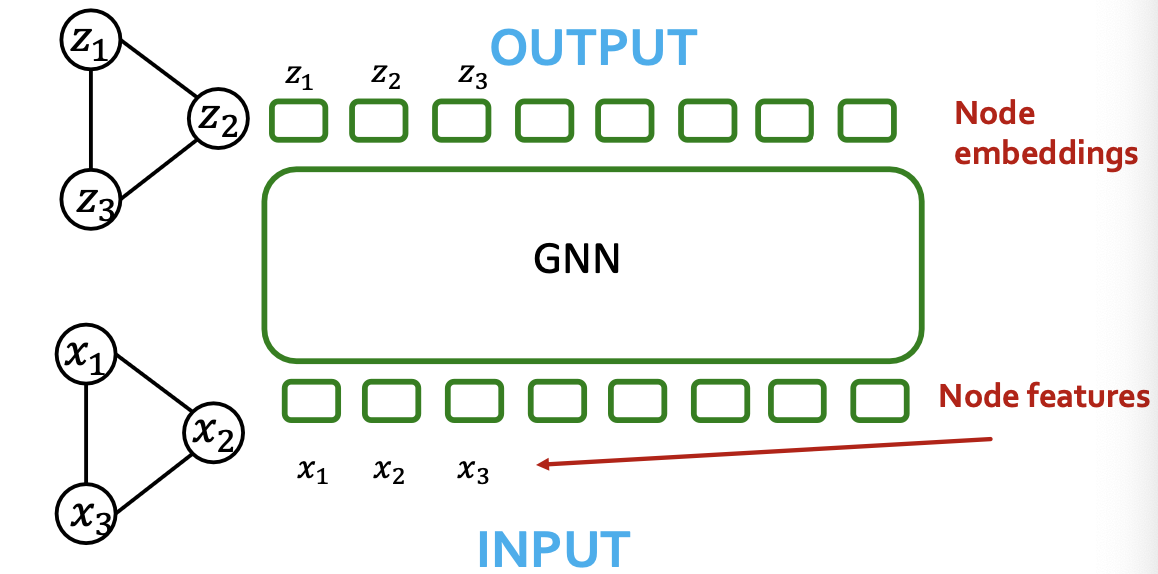
Are self-attention and message passing really different?

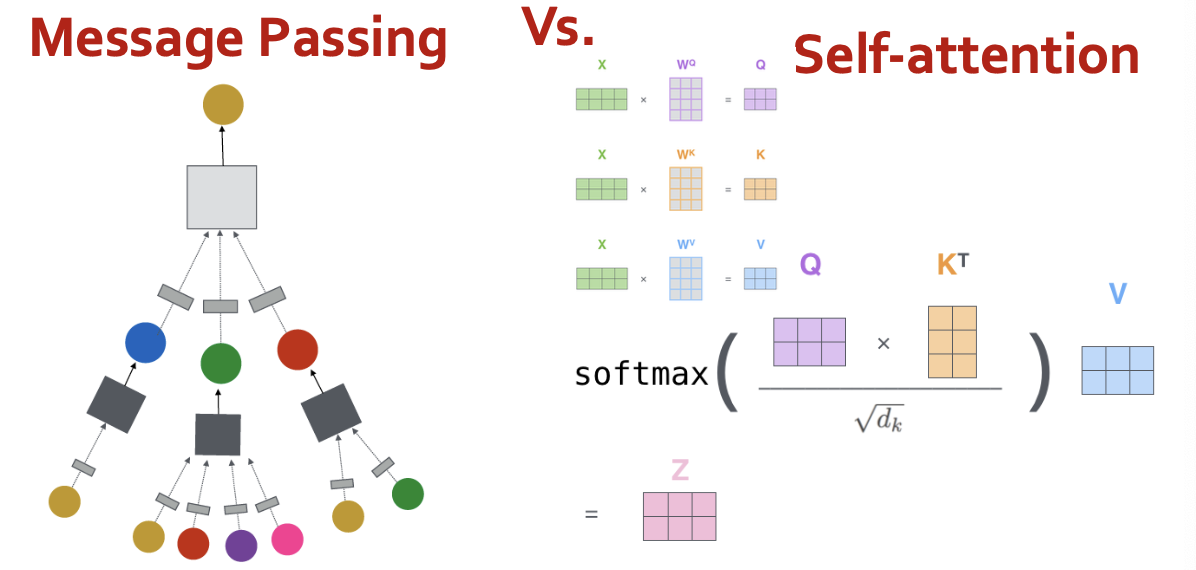
Self-attention vs. message passing

Interpreting the Self-Attention Update

Input stored row-wise $X = [- \ x_i\ -]$

Recall Formula for attention update:

\begin{align*}Att(X) &= softmax(K^TQ)V \\ &=softmax((XW^K)^T(XW^Q))XW^V \end{align*}

This formula gives the embedding for all tokens simultaneously

What if we simplify to just token $x_1$ ?

z_1 = \sum_{j=1}^5 softmax_j(q_1^Tk_j)v_j

If we simplify to just token $x_1$ what does the update look like?

z_1 = \sum_{j=1}^5 softmax_j(q_1^Tk_j)v_j

Steps for computing new embedding for token 1:
1. Compute message from $j$ : $MSG(x_j) = (v_j,k_j) = (W^Vx_j,W^Kx_j)$
1. Compute query for 1: $q_1 = W^Qx_1$
1. Aggregate all messages: $Agg(\{MSG(x_j):j\},q_1) = \sum_{j=1}^n softmax_j(q_1^Tk_j)v_j$

Self-Attention as Message Passing

Takeaway: Self-attention can be written as message + aggregation - i.e., it is a GNN!

But so far there is no graph - just tokens.
- So what graph is this a GNN on?

Clearly tokens = nodes, but what are the edges?

Key observation:
- Token 1 depends on (receives “message” from) all other tokens
- → the graph is fully connected!

Alternatively: if you only sum over $j \in N(i)$ you get ~ GAT

z_1 = \sum_{j=1}^5 softmax_j(q_1^Tk_j)v_j

Takeaway 1: Self-attention is a special case of message passing.

Takeaway 2: It is message passing on the fully connected graph.

Takeaway 3: Given a graph $G$ , if you constrain the self-attention softmax to only be over $j$ adjacent to $i$ nodes, you get ~ GAT!

A New Design Landscape for Graph Transformers

Processing Graphs with Transformers

We start with graph(s)

How to input a graph into a Transformer?

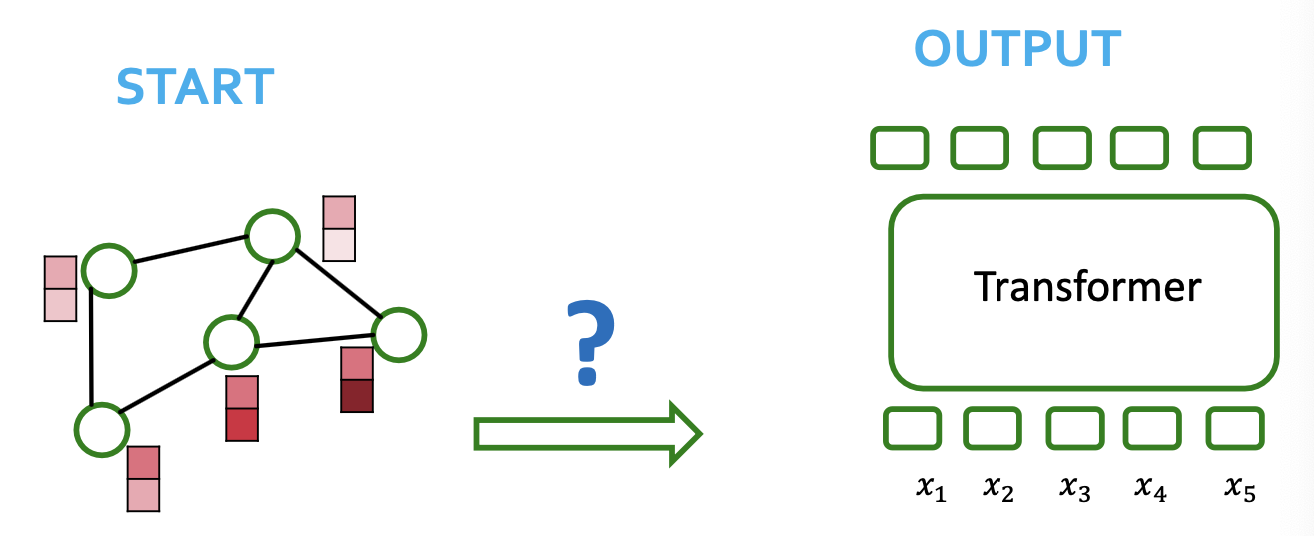
Components of a Transformer

Understand the key components of the Transformer. Seen already:
- tokenizing
- self-attention

Decide how to make suitable graph versions of each

A final key piece: token ordering

First recall update formula $z_1 = \sum_{j=1}^5 softmax_j(q_1^Tk_j)v_j$

Key Observation: order of tokens does not matter!!!

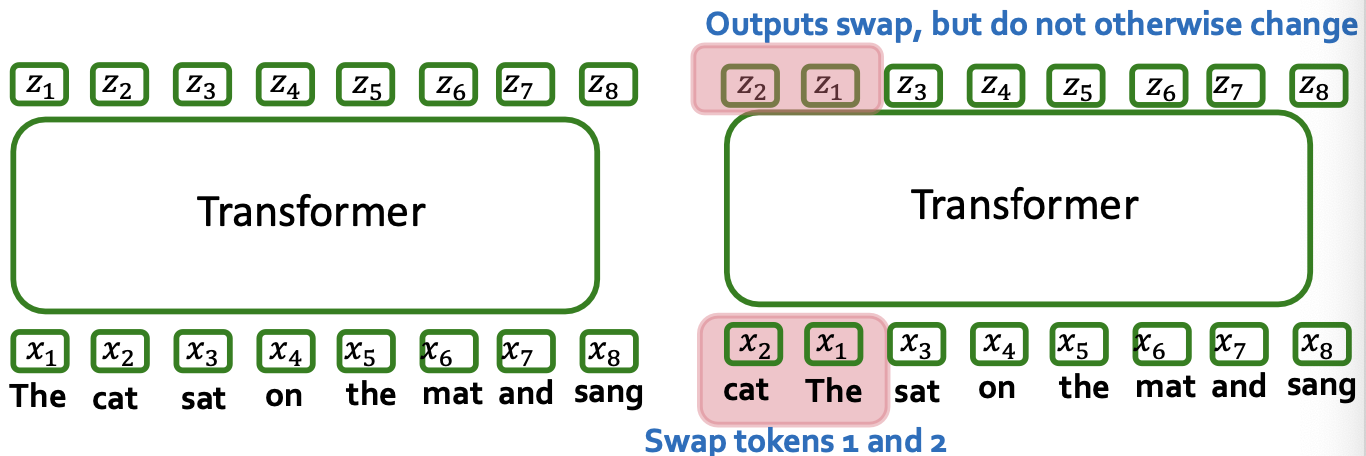
Same predictions no matter what order the words are in! (A “bag of words” prediction model) ….
- How to fix?

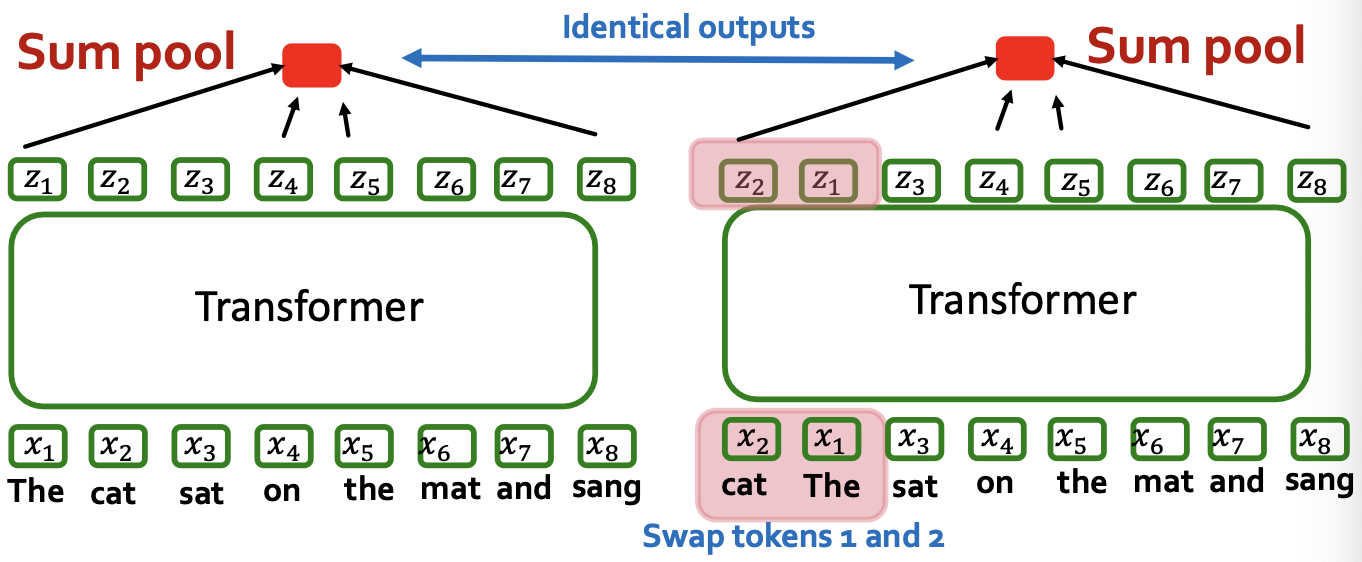
Positional Encodings

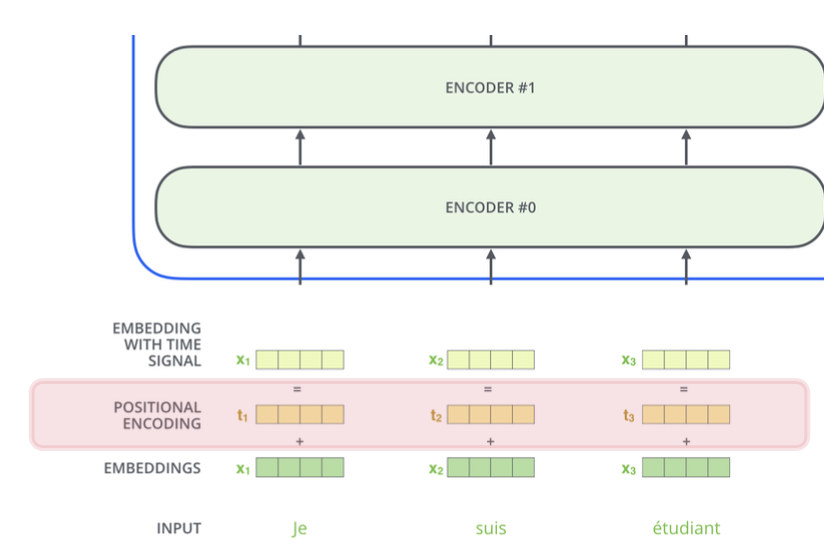
Transformer doesn’t know order of inputs

Extra positional features needed so it knows that
- Je = word 1
- suis = word 2
- etc.

For NLP, positional encoding vectors are learnable parameters

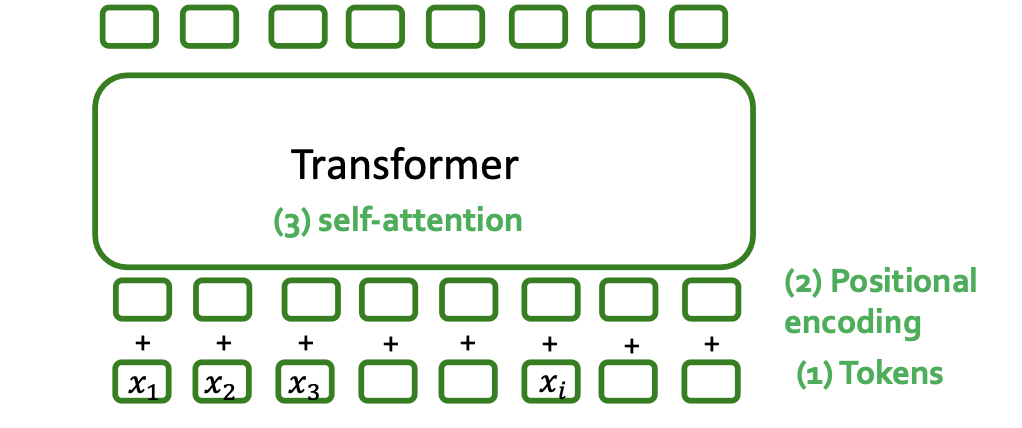
Components of a Transformer

Key components of Transformer
- Tokenizing
- Positional encoding
- Self-attention

Key question: What should these be for a graph input?

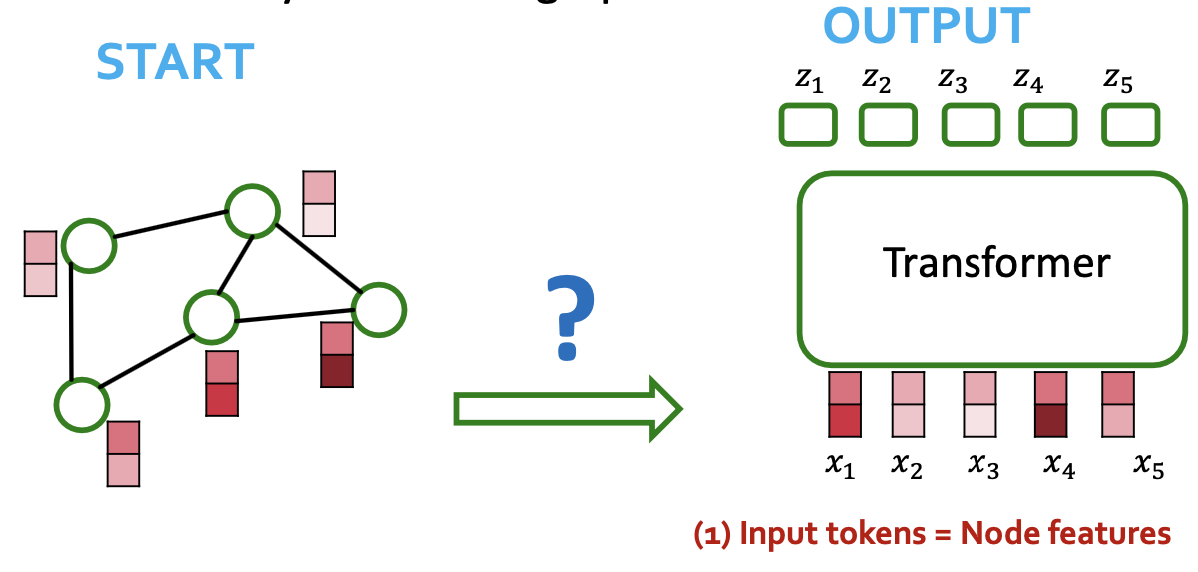
Processing Graphs with Transformers

A graph Transformer must take the following inputs:
- (1) Node features? → (1) Tokenizing
- (2) Adjacency information? → (2) Positional encoding
- (3) Edge features? → (3) Self-attention

There are many ways to do this

Different approaches correspond to different “matchings” between graph inputs (1), (2), (3) transformer components (1), (2), (3)

Node as Tokens

Q1: What should our tokens be?

Sensible Idea: node features = input tokens

This matches the setting for the “attention is message passing on the fully connected graph” observation

Problem: We completely lose adjacency information!
- How to also inject adjacency information?

How to Add Back Adjacency Information?

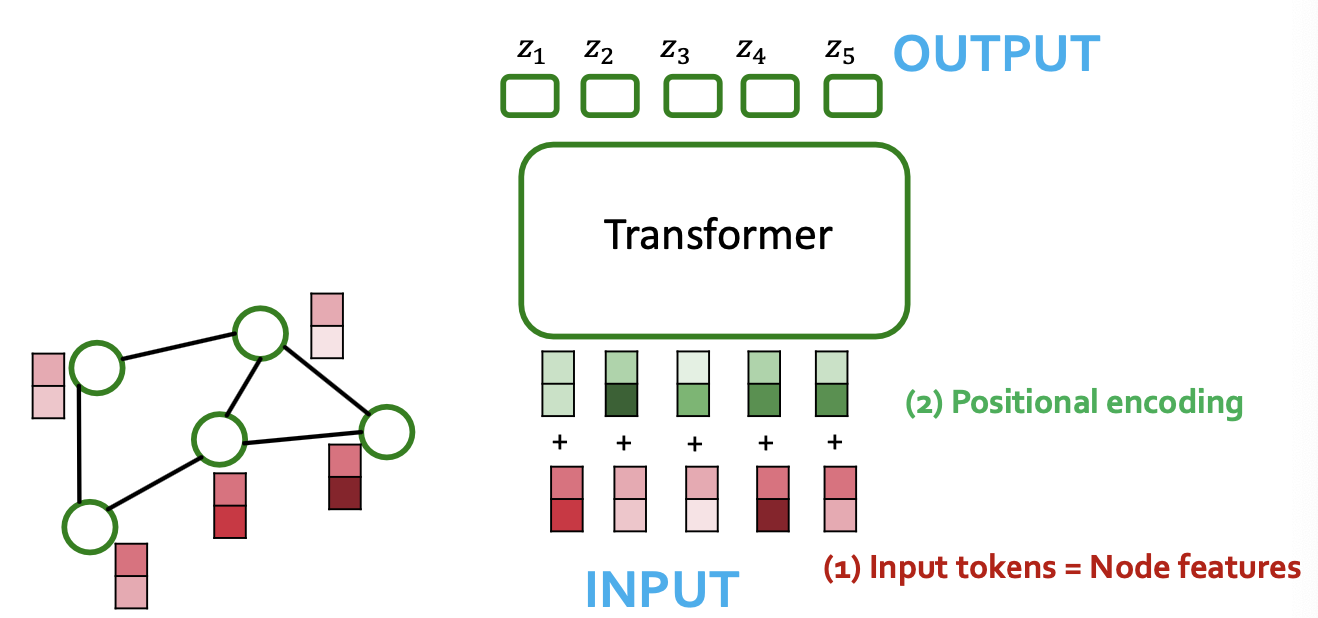
Idea: Encode adjacency info in the positional encoding for each node.

Positional encoding describes where a node is in the graph.

Q2: How to design a good positional encoding?

Option 1: Relative Distances

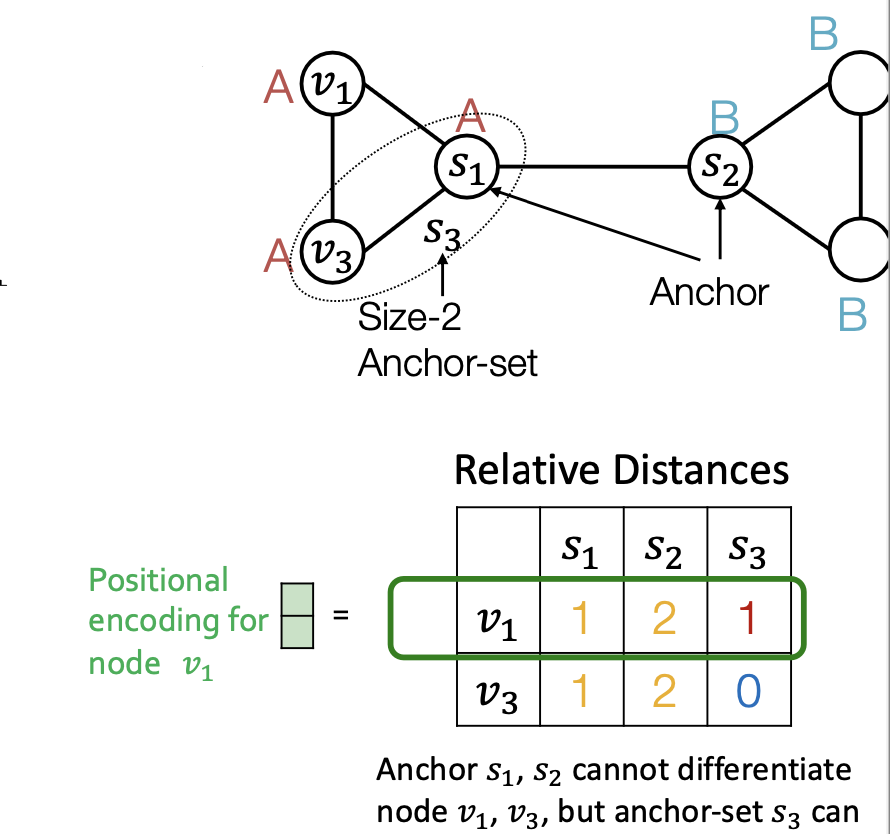
Last lecture: positional encoding based on relative distances

Similar methods based on random walk

This is a good idea! It works well on many cases

Especially strong for tasks that require counting cycles

Option 2: Laplacian Eigenvector Positional Encodings

Draw on knowledge of Graph Theory (many useful and powerful tools)

Key object: Laplacian Matrix $L = Degrees - Adjacency$
- Each graph has its own Laplacian matrix
- Laplacian encodes the graph structure
- Several Laplacian variants that add degree information differently

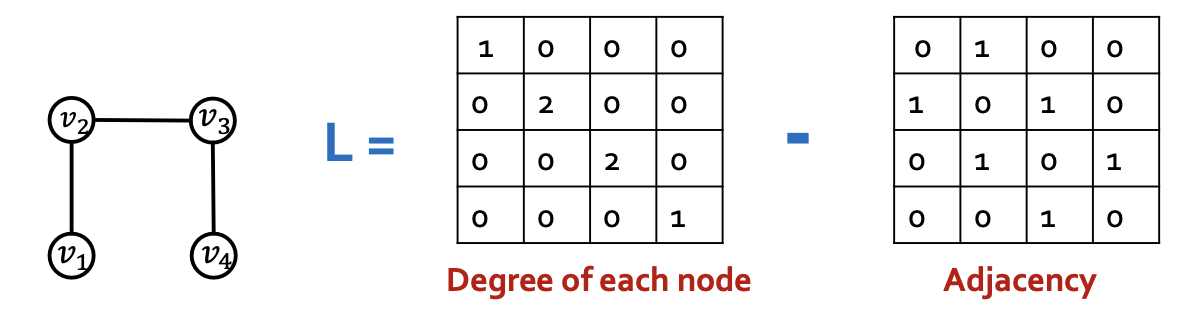
Laplacian matrix captures graph structure

Its eigenvectors inherit this structure

This is important because eigenvectors are vectors and so can be fed into a Transformer

Eigenvectors with small eigenvalue = local structure, large eigenvalue = global symmetries

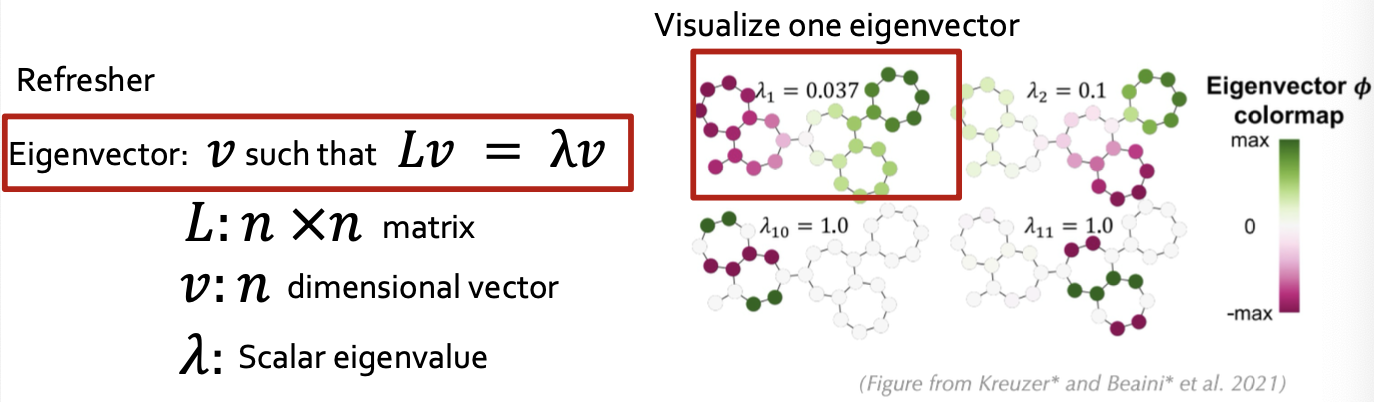
Positional Encoding Steps:

Compute $k$ eigenvectos

Stack into matrix

$i$ th row is positional encoding for node $i$

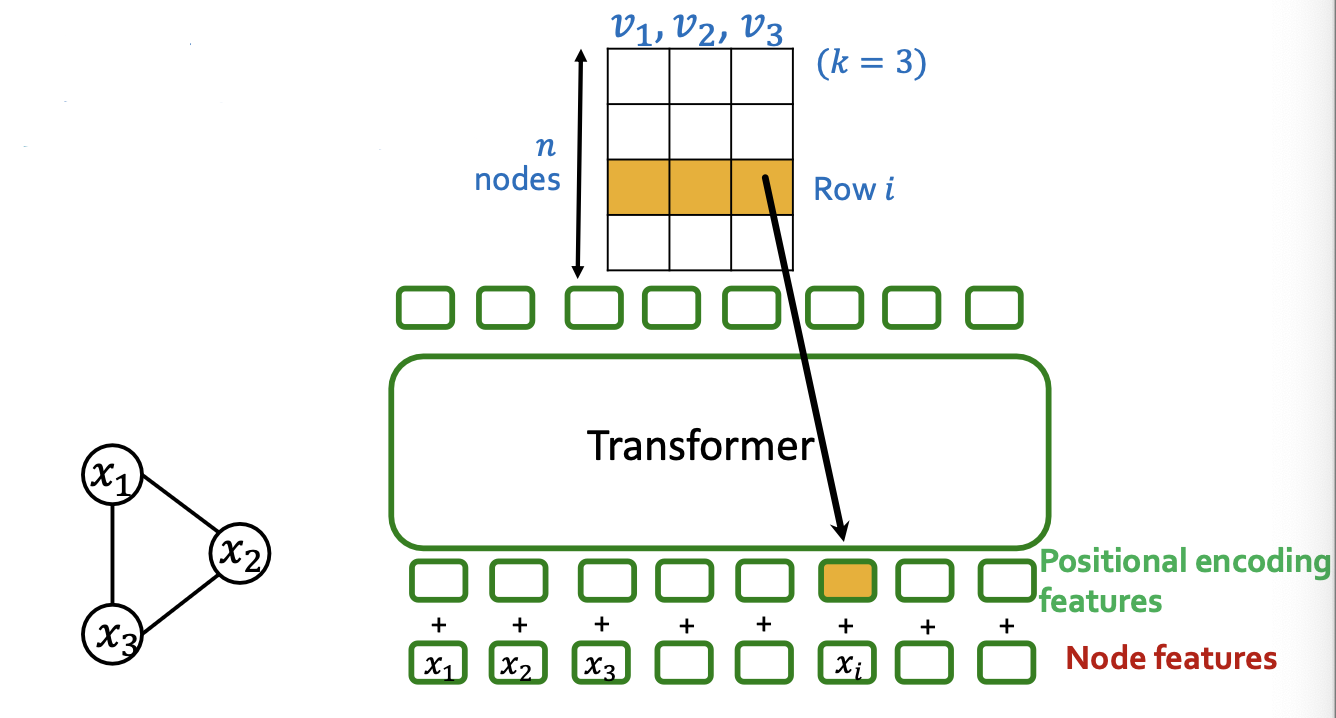
Laplacian Eigenvector positional encodings can also be used with message-passing GNNs

Edge Features in Self-Attention

Not clear how to add edge features in the tokens or positional encoding

How about in the attention?

Att(X) = softmax(K^TQ)V

$[k_{ij}] = K^TQ$ is an $n \times n$ matrix. Entry $k_{ij}$ describes “how much” token $j$ contributes to the update of token $i$ .

Idea: adjust $k_{ij}$ based on edge features. Replace with $k_{ij} + c_{ij}$ where $c_{ij}$ depends on the edge features

Implementation:
- If there is an edge between $i$ and $j$ with features $e_{ij}$ , define $c_{ij} = w_1^Te_{ij}$ (Learned parameters $w_1$ )
- If there is no edge, find shortest edge path between $i$ and $j$ $(e^1,e^2,\cdots,e^N)$ and define $c_{ij} = \sum_n w_n^T e^n$ (Learned parameters $w_1,\cdots,w_N$ )

Summary: Graph Transformer Design Space

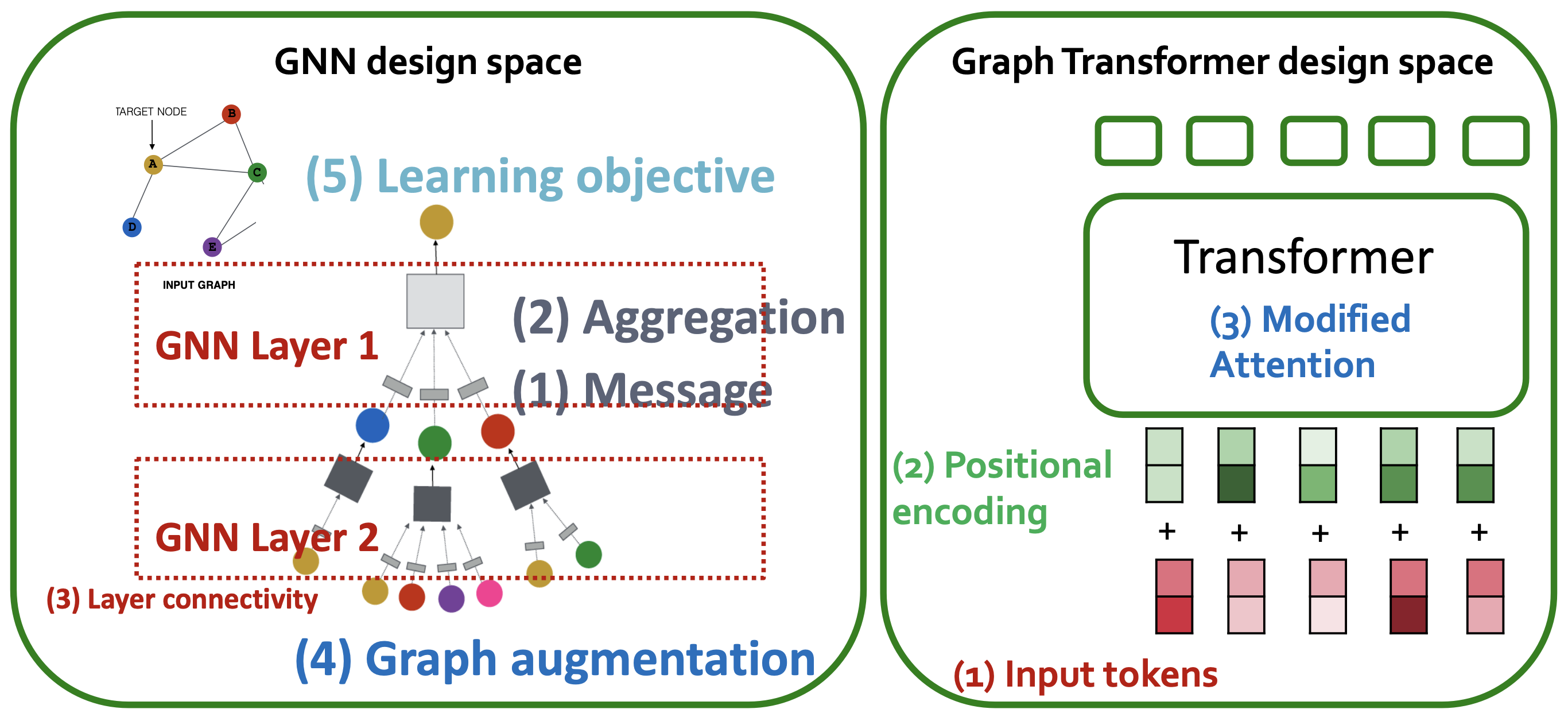
Tokenization
- Usually node features
- Other options, such as subgraphs, and node + edge features

Positional Encoding
- Relative Distances, or Laplacian eigenvectors
- Gives Transformer adjacency structure of graph

Modified Attention
- Re-weight attention using edge features