CS224W-Machine Learning with Graph-GNNs and Algorithmic Reasoning

GNNs and Algorithmic Reasoning

• $20^{th}$ century saw unprecedented development of algorithms
  • Sorting, shortest paths, graph search, routing
  • Algorithmic paradigms such as greedy, divide-and-conquer, parallelism, recursion, deterministic vs non-deterministic

Graph Machine Learning

How to learn mapping function $f$?

Connection to classical graph algorithms unclear.

• So far treated GNNs as a “new” type of graph algorithm.

• But in reality, graph ML has deep connections to the theory of computer science

Graph Neural Networks

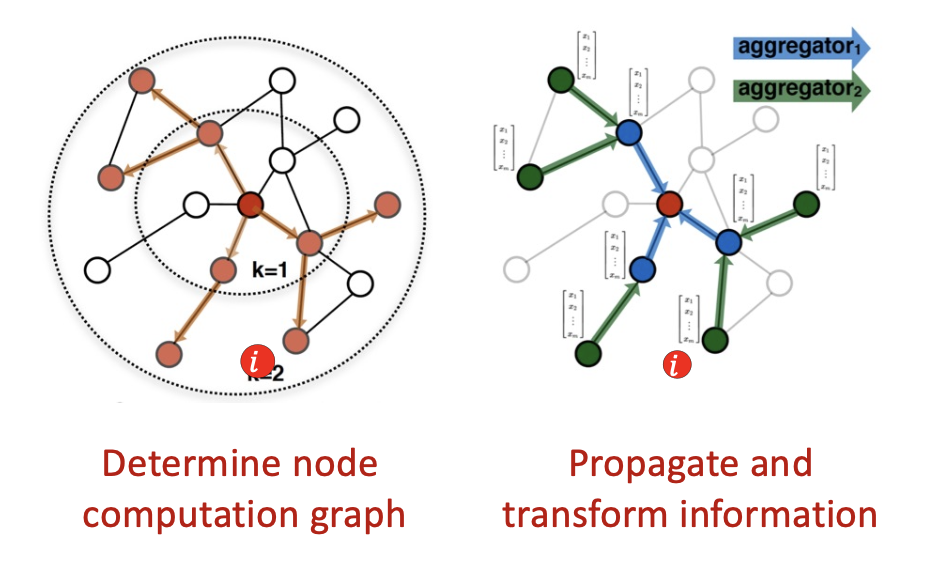
• GNNs defined by computation process

• I.e., how information is propagated across the graph to compute node embeddings

GNNs as graph algorithms

• We define “message passing” a computational process

• Message passing defines a class of algorithms on graphs

• But it’s not clear what algorithm(s)

• A clue to get started: We have already seen one algorithm GNNs can express…

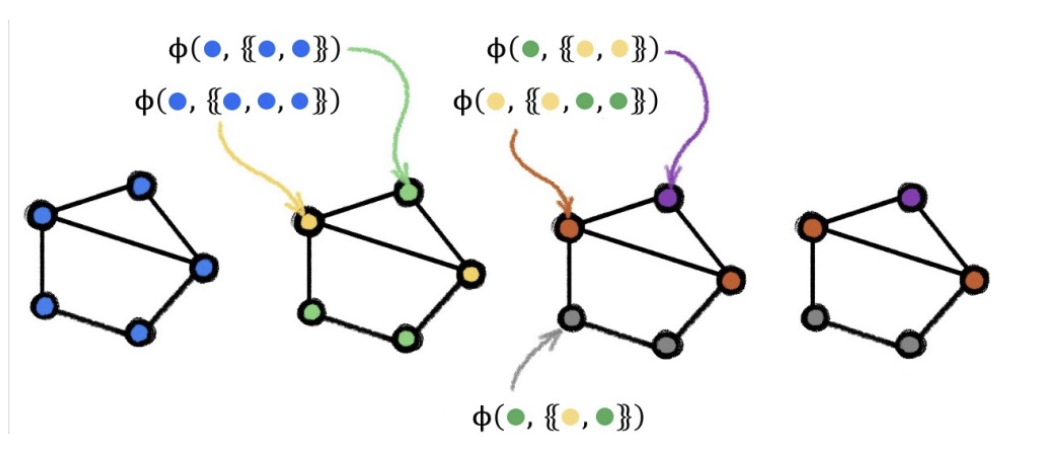
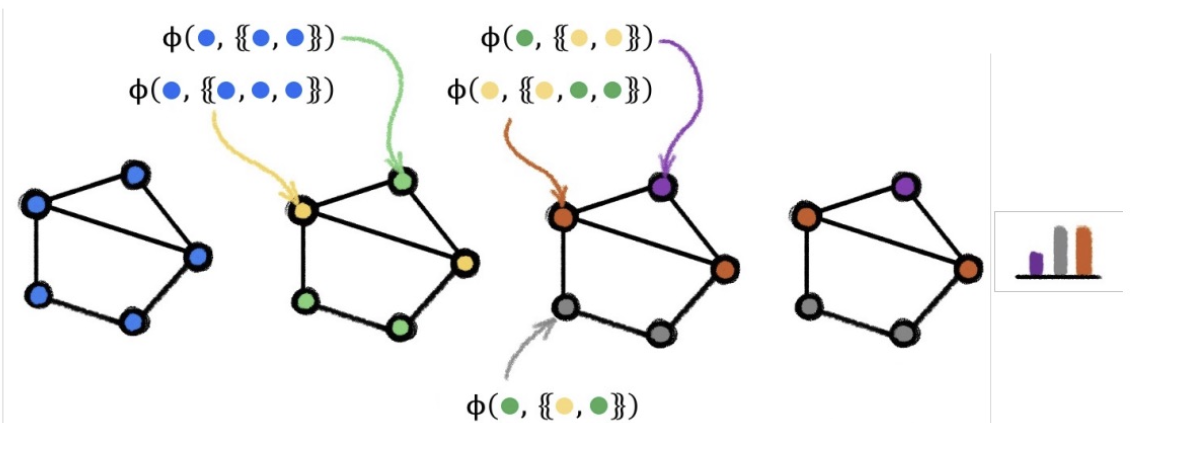
GNNs and the Weisfeiler-Lehman Isomorphism Test

• Simple test for testing if two graphs are the same:
  • Assign each node a “color”
  • Randomly hash neighbor colors until stable coloring obtained
  • Read out the final color histogram

• Declare two graphs:
  • Non-isomorphic if final color histograms differ
  • Test inconclusive otherwise ( i.e., we do not know for sure that two graphs are isomorphic if the counts are the same)

• Running the test…

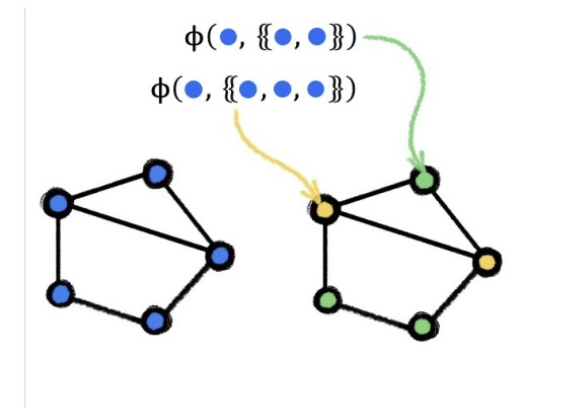
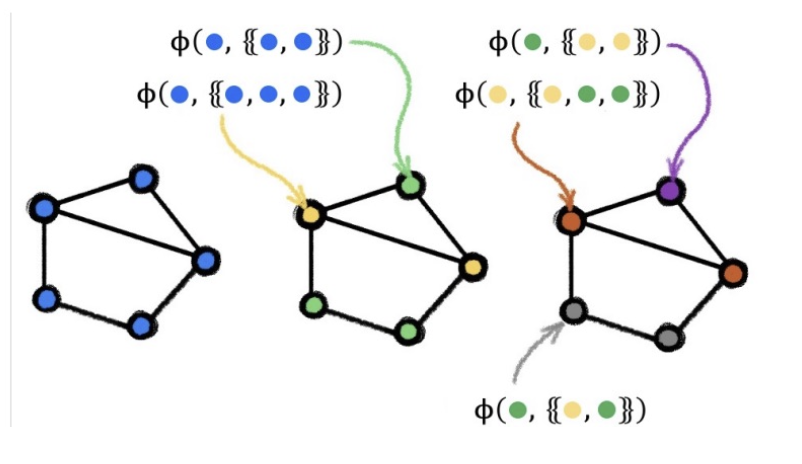
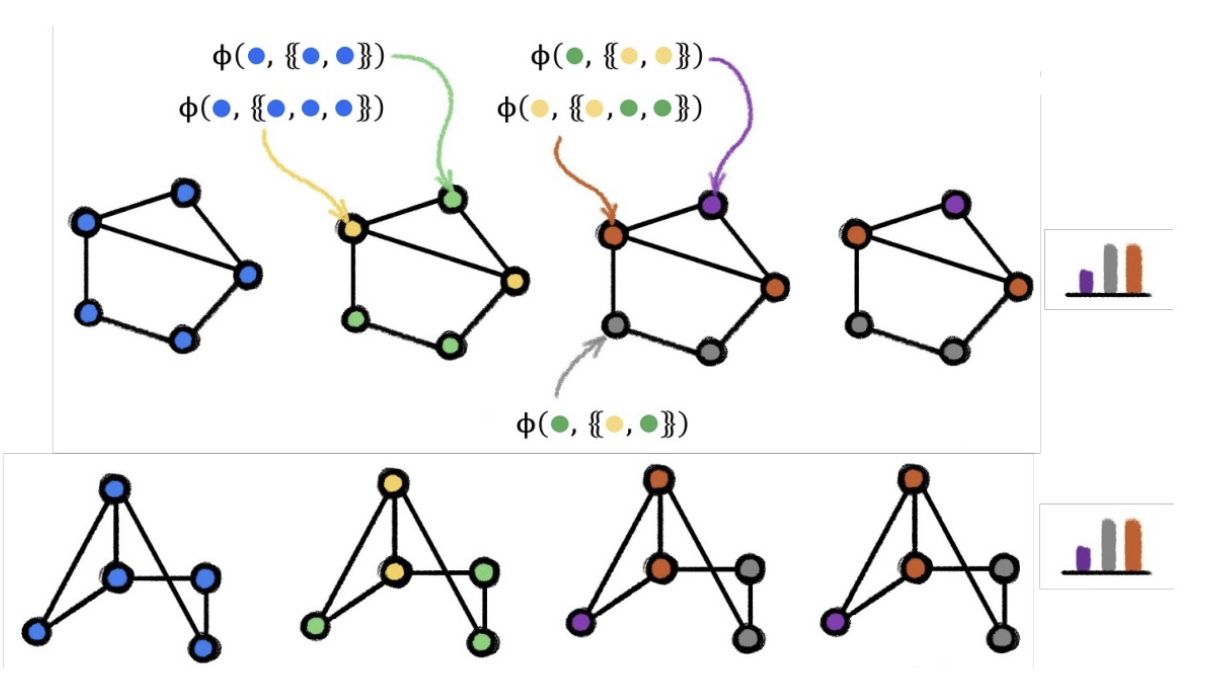
• We have seen GIN is as expressive as the 1-WL test
  • i.e., Given $G_1,G_2$, the following are equivalent:
    • there exist parameters s.t. $GIN(G_1) \neq GIN(G_2)$
    • 1-WL distinguishes $G_1,G_2$’

• GIN is a “neural version” of the 1-WL algorithm
  • Replaces HASH function with learnable MLP

• But this does not mean that 1-WL is the only graph algorithm GNNs can simulate.

• An untrained GNN (random MLP = random hash) is close to the 1-WL test.

Algorithmic structure of neural networks

• A neural network architecture defines a learnable computer program

• Key intuition:
  • MLPs easily learn smooth functions (e.g., linear, log, exp)
  • MLPs bad at learning complex function (e.g., sums of smooth functions - i.e., for-loops)

• Approach: define progressively more complex algorithmic problems, and corresponding neural net architectures capable of solving each.

Neural Nets and Algorithm Structure

• Problem 1 (feature extraction):
  • Input: “flat” features $\textbf{x} \in \mathbb{R}^n$ (e.g., color, size, position)
  • Output: scalar value $\textbf{y}$ (e.g., is it round and yellow?)

• No other prior knowledge (minimal assumptions)

• Q: What neural network choice suits this problem?

• A: MLPs (multilayer perceptrons)
  • Universal approximator
  • Makes no assumptions on input/output structure.

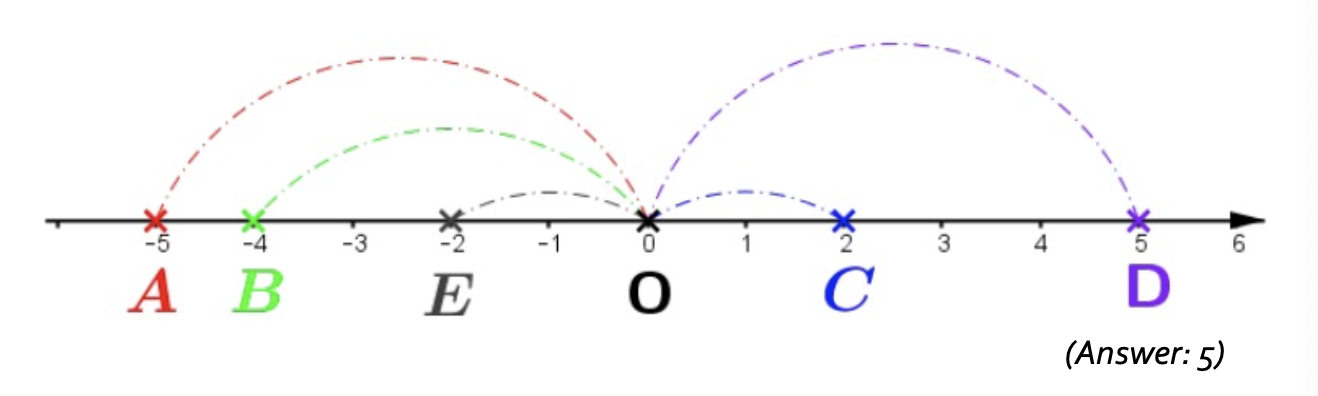
• Problem 2 (summary statistics):
  • Input: a set of objects $\{x_i\}$, each with features containing their coordinate and color $x_i = [x_i^{color},x_i^{coordinate}]$
  • Task Output: some aggregate property of the set (e.g., largest x-coordinate)
  • $y(\{x_i\}) = max_i (x_i^{coordinate})$

  

  • MLP model: $MLP(x_1,\cdots,x_n)$
  • Not well suited to this task
  • To learn max (and min) MLP has to learn to execute a for-loop
  • This is a complex operation, MLP needs lots of data to learn
  • New Deepset model:
    • $\text{DeepSet}(\{x_i\}) = \text{MLP}_1 (\sum_i\text{MLP}_2(x_i))$
  • Well suited to this task
  • Can approxmator softmax, a simple approx. to min/max
    • $max_i(x_i^{coordinate}) \approx log(\sum_i e^{x_i^{coordinate}})(MLP_1 \ learns \ log,MLP_2 \ learns \ exp)$
  • Key points:
    • Consequence: MLPs only must learn simple functions (log/exp)
    • This can be done easily, without needing much data
  • MLP can provably also learn this. But must learn complex for-loop, which requires lots of training data

  

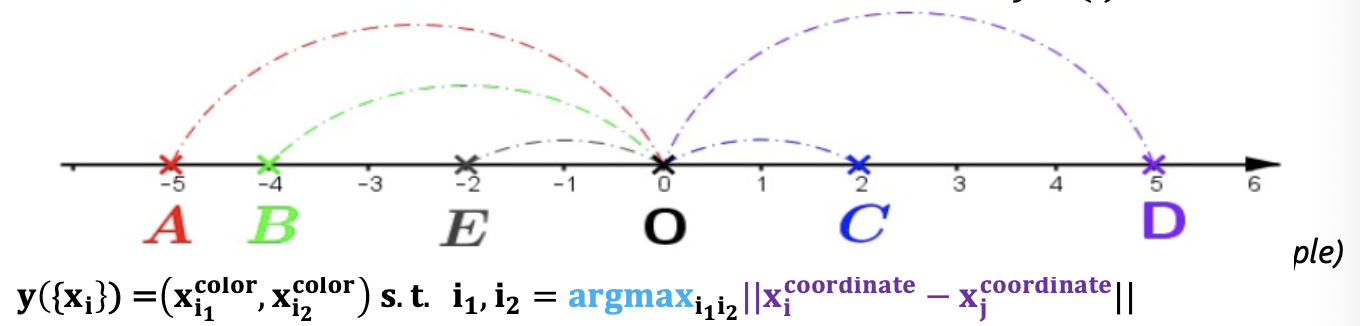
• Problem 3 (relational argmax)
  • Input: a set of objects $\{x_i\}$, each with features containing their coordinate and color $x_i = [x_i^{color},x_i^{coordinate}]$

  

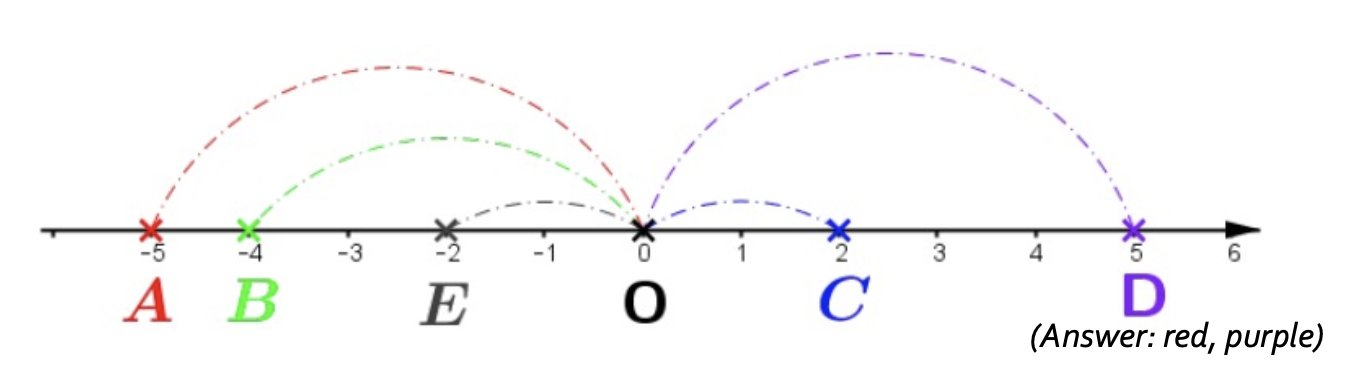
  • Task Output: property of pairwise relation (e.g., what are the colors of the two furthest away objects?)
  • $y(\{x_i\}) = (x_{i_1}^{color},x_{i_2}^{color})$ s.t., $i_1,i_2 = argmax_{i_1,i_2}||x_i^{coordinate}- x_{j}^{coordinate}||$
  • DeepSet poorly suited to modelling pairwise relations
    • Recall: $\text{DeepSet}(\{x_i\}) = \text{MLP}_1 (\sum_i\text{MLP}_2(x_i))$
  • Reason:
    • task requires comparing pairs of objects - i.e., a for-loop
    • each object processed independently by $MLP_1$
    • Consequence: $MLP_2$ has to learn complex for-loop (hard)
  • $\sum_iMLP_1(x_i)$ provably cannot learn pairwise relations Theorem: Suppose $g(x,y)=0$ if and only if $x=y$. Then there is no $f$ such that $g(x,y)= f(x)+f(y)$
  • GNN well suited to this task: for-loop is built in!
    • E.g., recall GIN update
    • For $i = 1,\cdots,n:$
      • $h_i^{l+1} = MLP_2 (MLP_1(h_i^l)+\sum_{j\in N(i)}MLP_1(h_j^l))$

    • Update of node embedding depends on other nodes
      • $MLP_1$ computes distance from $i$ to $j$
      • $MLP_2$ identifies which pair is best in $\{(i,j)\}_{j \in N(i)}$

      

  

General algorithm class for GNN?

• GNNs are good at solving tasks that require relating pairs of objects (nodes)
  • MLPs/DeepSets cannot do this easily since they have to learn for-loop

• “Relational argmax” is just one problem that GNN can solve….

Algorithmic Class of GNNs

Dynamic Programming

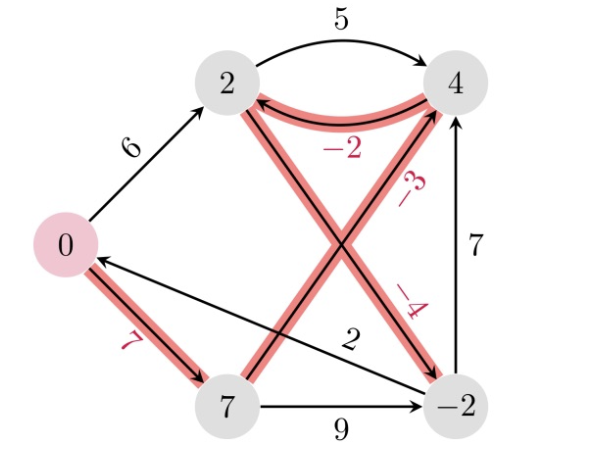
• Task 4 (shortest path):
  • Input: a weighted graph and a chosen source node
  • Output: all shortest paths out of source node (shortest path tree)

  

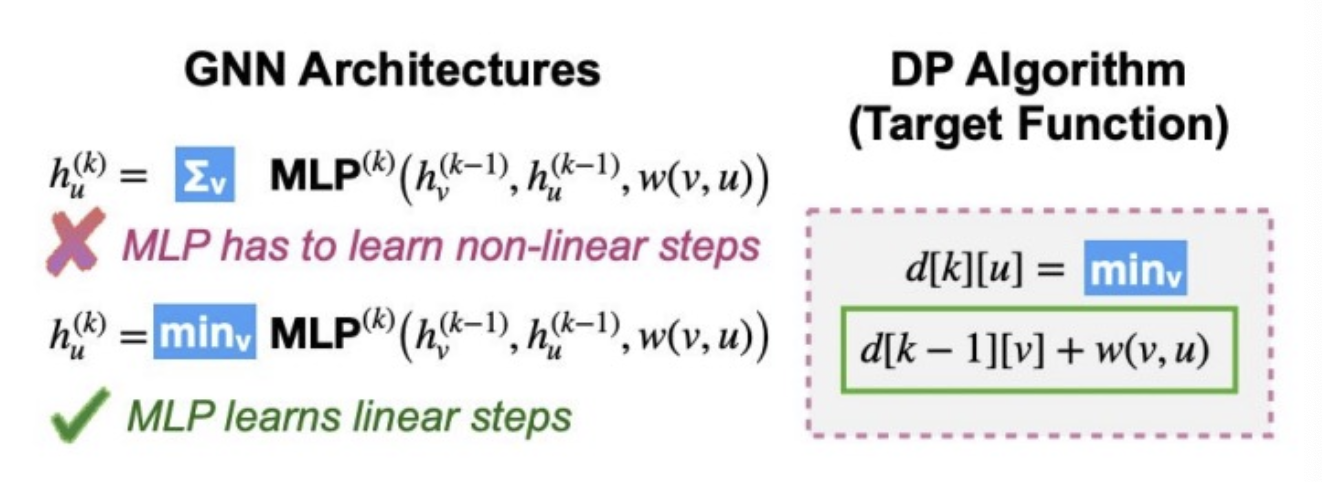
GNN are Dynamic Programs

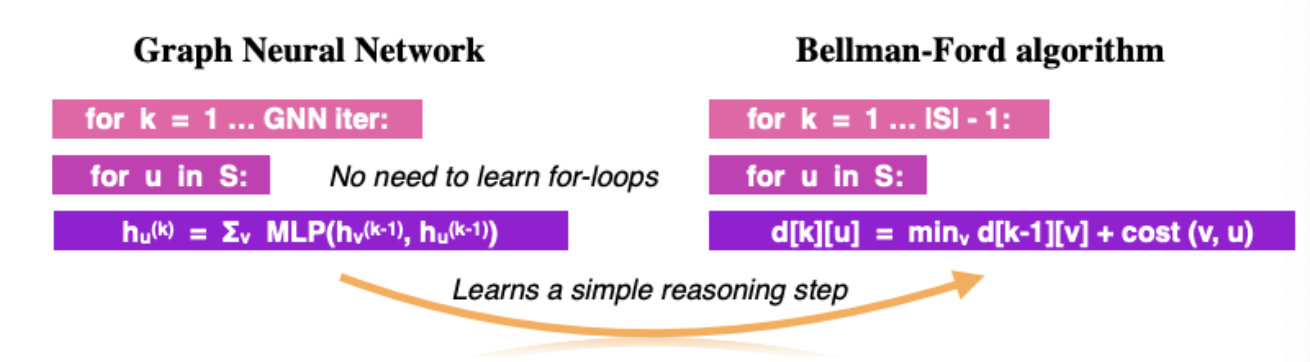
• Dynamic programming has very similar form to GNN

• Both have nested for-loops over:
  • Number of GNN layers / iterations of BF
  • Each node in graph

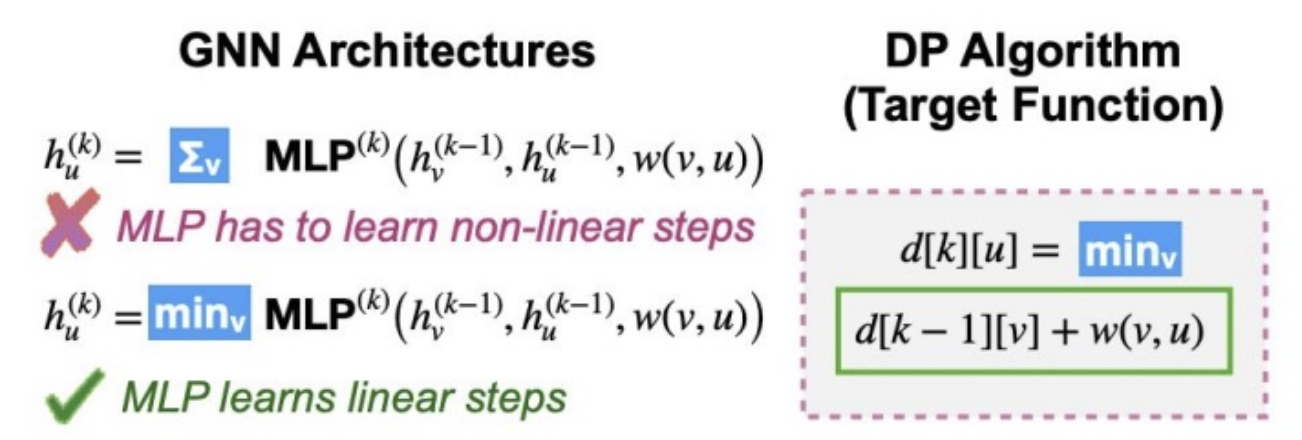
• GNN aggregation + MLP only needs to learn sum + min

• An MLP trying to learn a DP has to learn double-nested for loop (really hard to do)

• There is an even better choice of GNN..
  • Choose min activation to match DP
  • Then MLP only needs to learn linear function!

  

Algorithmic Alignment

Algorithmic-Centric Principle For Neural Network Design

• In the previous section we studied what type of tasks GNN excel at solving
  • Key idea: Focus on the algorithm that solves the tasks
  • If the neural net can express the algorithm easily, then it’s a good choice of architecture.

Algorithmic Alignment

Given a target algorithm $g = g_m \circ \cdots g_1$, a neural network architecture $f = f_m \circ \cdots f_1$ if:

• $g_i$ a simple function

• $f_i$ can express $g_i$

• Each $f_i$ has few learnable parameters. (so can learn $g_i$ easily)

Designing New Neural Nets with Algorithmic Alignment

• GNN is algorithmically aligned to dynamic programming (DP)

• But algorithmic alignment is a general principle for designing neural network architectures

• So we should be able to use it to design entirely new neural networks given a particular problem

• Many successful example of this in this

Applications of Algorithmic Alignment

• Application 1: building a network to solve a new task
  • The subset-sum problem (NP-hard)

• Application 2: building neural networks that can generalize out-of-distribution
  • The linear algorithmic alignment hypothesis

Solving an NP-hard Task: Subset Sum

• Task: given a set of number $\mathcal{S}$, decide if there exists a subset that sums to $k$.

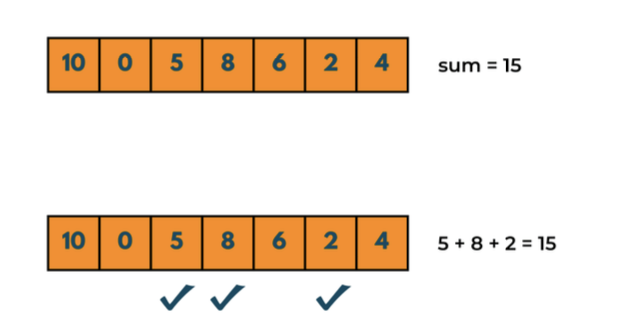
• Known to be NP-hard, no DP algorithm can solve this (so GNN not suitable)

• Exhaustive Search Algorithm for solving subset sum:
  • Loop over all subset $\tau \in S$ and check is sum is $k$

• Clearly not polynomial time… but can it inspire a neural net architecture?

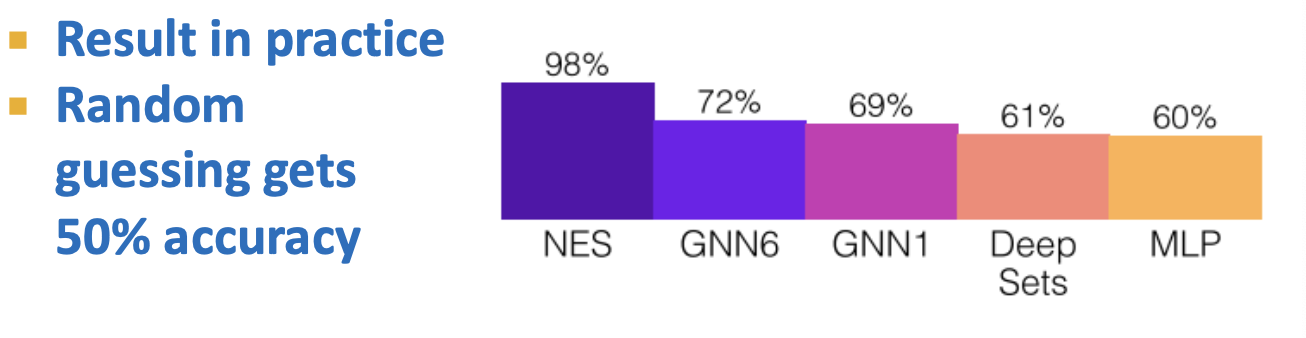
• Neural Exhaustive Search:
  • Given $S = \{X_1,\cdots,X_n\}$,
  • $NES(S) = MLP (\max\limits_{\tau \subseteq S } LSTM(X_1,\cdots,X_{|\tau|}:X_1,\cdots,X_{|\tau|}\in \tau) )$
    • Algorithmically aligned to exhaustive search:
      • LSTM learns if the sum $X_1+\cdots+X_{|\tau|} = k$ (simple function)
      • Max aggregation identifies best subset
      • MLP maps to true/false value

Algorithmic Alignment and Extrapolation

• We have argued that algorithmic alignment can help inspire architectures well suited to particular tasks
  • By well suited, we mean generalizes well using little training data

• But true AI requires something stronger than this…
  • Also needs to “extrapolate” to instances that look very different from the training data

• Extrapolation is also called out-of-distribution generalization

• Extrapolation is a holy grail of AI, necessary for systems to behave reliably in unforeseen future situations

How MLPs extrapolate

• Observation: ReLU MLPs extrapolate linearly

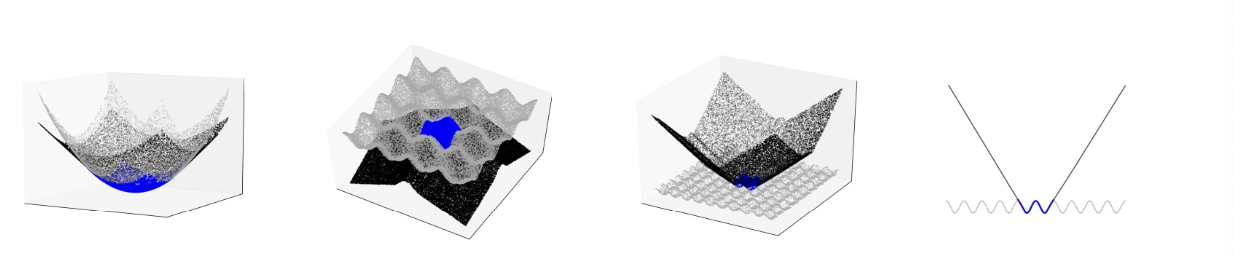
• Can be proved that extrapolation is perfect for linear target functions

• But ReLU MLPs cannot generalize for non-linear target functions…

• The need for linearity for MLP extrapolation suggests a hypothesis for GNN extrapolation…

The Linear Algorithmic Alignment Hypothesis

• Linear Algorithmic Alignment Hypothesis

Linear algorithmic alignment implies a neural network can extrapolate to unseen data

• Linear Algorithmic Alignment

Given a target algorithm $g = g_m \circ \cdots g_1$, a neural network architecture $f = f_m \circ \cdots f_1$ linearly aligns if:

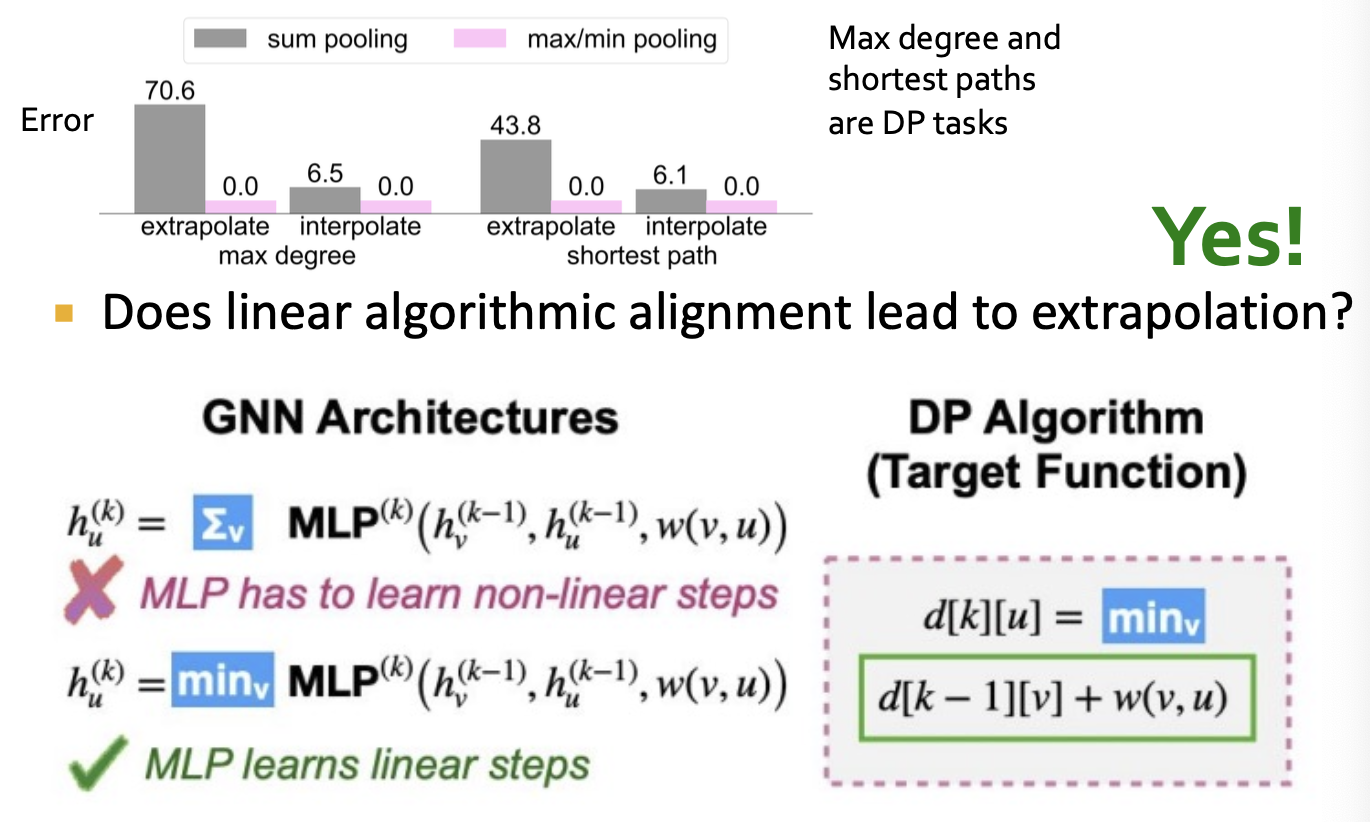
How GNNs extrapolate

• Recall GNN for learning dynamic programs

• GNN aggregation function is key
  • Min aggregation is linearly algorithmically aligned
  • Sum aggregation is not

• Does linear algorithmic alignment lead to extrapolation?