CS224W-Machine Learning with Graph-Node Embeddings

Traditional ML for Graphs

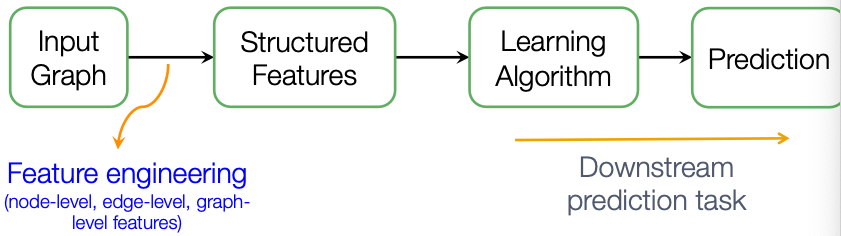
Given an input graph, extract node, link and graph-level features, then learn a model (SVM, neural network, etc.) that maps features to labels.

Graph Representation Learning(图表示学习)

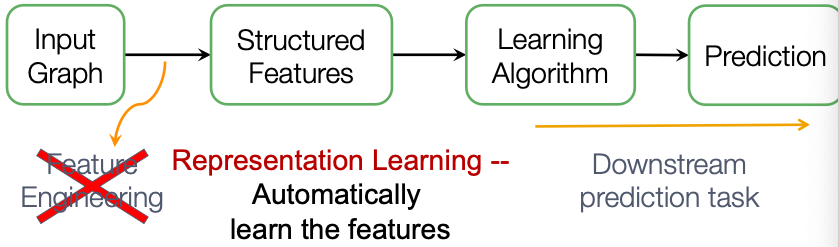
Graph Representation Learning alleviates the need to do feature engineering every single time.

Goal: Efficient task-independent feature learning for machine learning with graphs! (不需要特征学习)

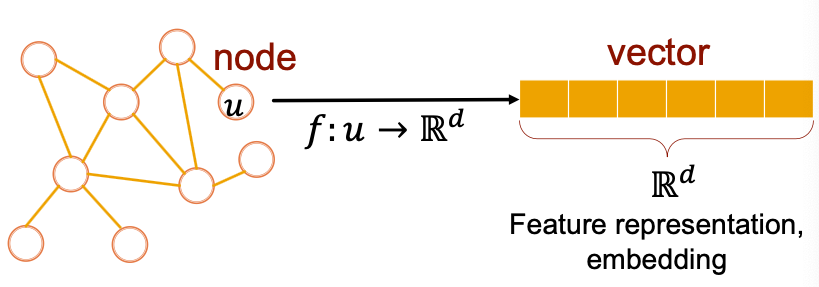
Why Embedding? (为什么需要嵌入？)

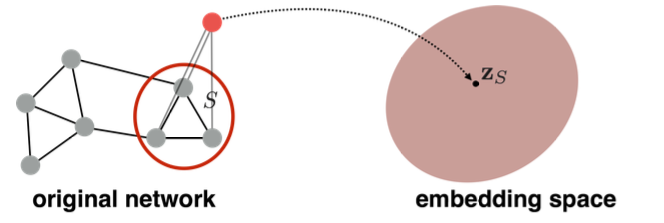
Task: Map nodes into an embedding space

Similarity of embeddings between nodes indicates their similarity in the network.
- Both nodes are close to each other (connected by an edge)

Encode network information

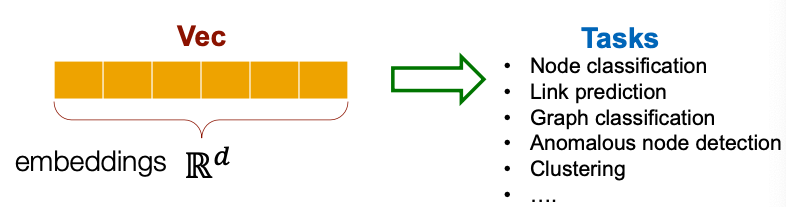
Potentially used for many downstream predictions (可用于许多下游预测任务)

Encoder and Decoder

Setup

$V$ is the vertex set.

A is the adjacency matrix (assume binary)

V:\{1,2,3,4\}\\ A = \begin{pmatrix} 0&1&0&1\\1&0&0&1\\0&0&0&1\\1&1&1&0 \end{pmatrix}

Embedding Nodes

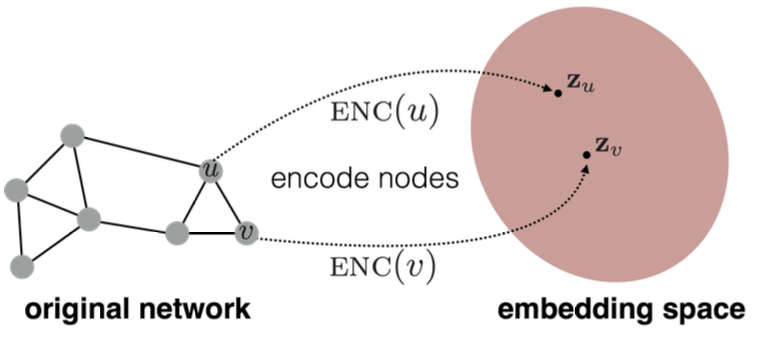
Goal is to encode nodes so that similarity in the embedding space (e.g., dot product) approximates similarity in the graph.

Goal:\ similarity(u,v) \approx \textbf{}z_v^T \textbf{z}_u

Learning Node Embedding (节点嵌入)

Encoder maps from nodes to embeddings

Define a node similarity function (i.e., a measure of similarity in the original network)

Decoder $DEC$ maps from embeddings to the similarity score

Optimize the parameters of the encoder to that $DEC(\textbf{z}^T_v\textbf{z}_u)$

similarity(u,v) \approx \textbf{}z_v^T \textbf{z}_u

两个关键部分 Encoder + Decoder

Encoder: maps each node to a low-dimensional vector
$ENC(v) = \textbf{z}_v$
- $v$ node in the input graph
- $\textbf{z}_v$ d-dimensional embedding

Similarity function: specifies how the relationships in vector space map to the relationships in the original network
$\text{Decoder} \\ \textbf{similarity}(u,v) \approx \textbf{z}^T_v \textbf{z}_u$
- 左: Similarity of $u$ and $v$ in the original network
- 右: dot product between node embeddings

“Shallow” Encoding

Simplest encoding approach: Encoder is just an embedding-lookup

ENC(v) = \textbf{z}_v = \textbf{Z} \cdot v

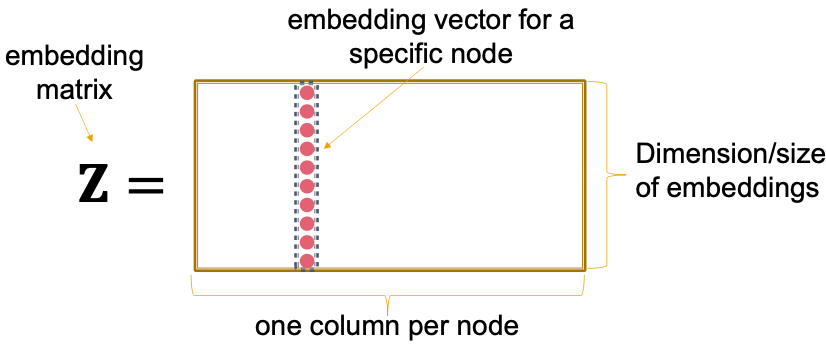
Matrix, each column is a node embedding [what we learn/ optimize]

\textbf{Z} \in \mathbb{R}^{d \times |\mathcal{V}|}

Indicator vector, all zeroes except a one in column indicating node

v \in \mathbb{I}^{|\mathcal{V}|}

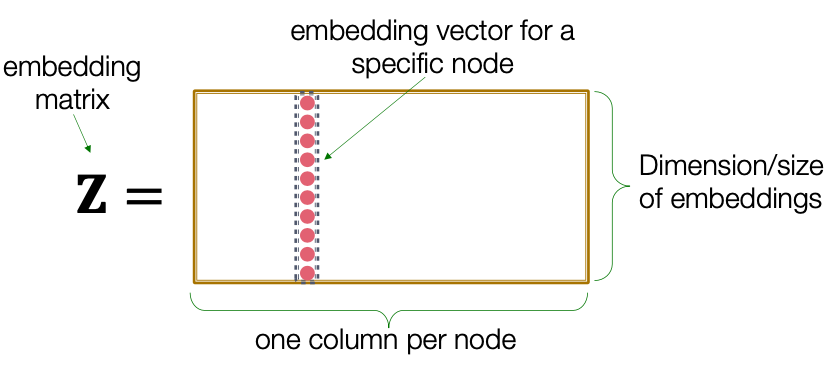
Each node is assigned a unique embedding vector

Framework Summary

Encoder + Decoder Framework
- Shallow encoder: Embedding lookup
- Parameters to optimize: $\textbf{Z}$ which contains node embeddings $\textbf{z}_u$ for all nodes $u \in V$
- We will cover deep encoders in the GNNs
- Decoder: based on node similarity
- Objective: maximize $\textbf{z}^T_v \textbf{z}_u$ for node pairs $(u,v)$ that are similar

Random Walk Approaches for Node Embeddings

Notation

Vector $\textbf{z}_u$ : The embedding of node $u$ (what we aim to find.)

Probability $P(v|\textbf{z}_u)$ : The (predicted) probability of visiting node $v$ on random walks starting from node $u$ .

Non-Linear functions used to produce predicted probabilities

Softmax function: Turn vector of $K$ real values (model predictions) into $K$ probabilities that sum to $1$ : $S(\textbf{z})[i] = \frac{e^{\textbf{z}[i]}}{\sum_{j=1}^{K}e^{\textbf{z}[j]}}$

Sigmoid function: S-shaped function that turns real values into the range of $(0,1)$ . Written as $\sigma(x) = \frac{1}{1+e^{-x}}$

Random Walk

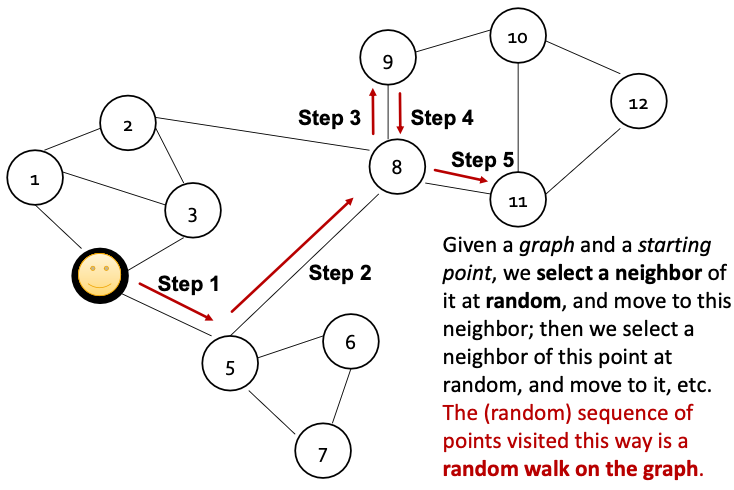
Random-Walk Embeddings

\textbf{z}^T_u \textbf{z}_v \approx \text{Probability that}\ u \ \text{and} \ v \ \text{co-occur on a random walk over the graph}

Random-Walk Embeddings

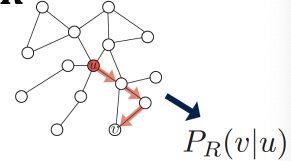
Estimate probability of visiting node $v$ on a random walk starting from node $u$ using some random walk strategy $R$ .

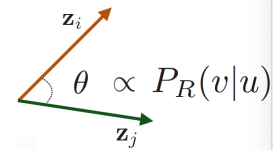
Optimize embeddings to encode these random walk statistics
Similarity in embedding space (Here: dot product $dot\ product = cos(\theta)$ ) encodes random walk “similarity”

为什么使用随机步嵌入？ (Why Random Walks?)

Expressivity: Flexible stochastic definition of node similarity that incorporates both local and higher-order neighbourhood information.

Efficiency: Do not need to consider all node pairs when training; only need to consider pairs that co-occur on random walks.

无监督特征学习（Unsupervised Feature Learning）

Intuition: Find embedding of nodes in $d-dimensional$ space that preserves similarity.

Idea: Learn node embedding such that nearby nodes are close together in the network.

? How do we define nearby nodes? $N_{R}(u)$ neighbourhood of $u$ obtained by some random walk strategy $R$ .

Feature Learning as Optimization

Given $G = (V,E)$

Our goal is to learn a mapping $f: u \rightarrow \mathbb{R}^d: f(u) = \textbf{z}_u$

Log-likelihood objective:

\argmax_{z} \sum_{u \in V} \log P(N_R(u)|\textbf{z}_u)

Given node $u$ , we want to learn feature representations that are predictive of the nodes in its random walk neighbourhood $N_{R}(u)$ .

随机步优化(Random Walk Optimization)

Run short fixed-length random walks starting from each node $u$ in the path using some random walk strategy $R.$

For each node $u$ collect $N_{R}(u)$ , the multiset of nodes visited on random walks starting from $u.$

Optimize embeddings according to: Given node $u$ , predict its neighbours $N_{R}(u)$ .

see Log-likelihood. $N_{R}(u)$ 其中可以含有重复的节点。因为随机步可能多次到达相同的点。

\argmax_z \sum_{u \in V} \log P(N_R(u)|\textbf{z}_u)\\ \Longrightarrow \argmax_z \mathcal{L} = \sum_{u \in V} \sum_{v \in N_R{u}} -\log(P(v|\textbf{z}_u))

直觉可以使用负对数似然估计。

Parameterize $P(v|\textbf{z}_u)$ using softmax:

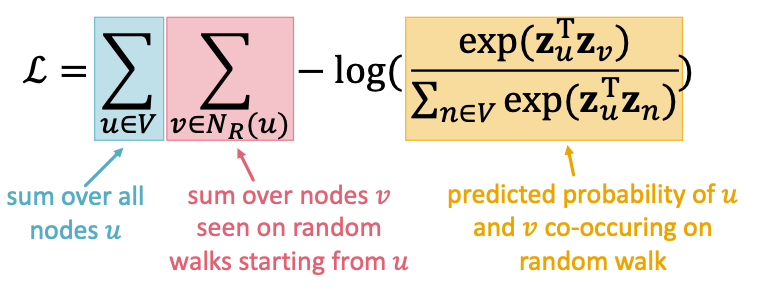
P(v|\textbf{z}_u) = \frac{e^{\textbf{z}^T_u\textbf{z}_v}}{\sum_{n \in V} e^{\textbf{z}^T_u \textbf{z}_n}}

如果要这么计算耗费太高，如果使用别的方法解决这个问题？

Solution: Negative Sampling (负采样)

-\log (\frac{exp(\textbf{z}^T_u \textbf{z}_v)}{\sum_{n \in V} exp(\textbf{z}^T_u \textbf{z}_n)}) \\ \approx \log (\sigma(\textbf{z}^T_u \textbf{z}_n)) + \sum_{i=1}^k \log (\sigma(-\textbf{z}^T_u \textbf{z}_n)), n_i \sim P_V

Sample $k$ negative nodes $n_i$ each with probability. proportional to its degree.

关于负采样，需要考虑的两个方面
- Higher $k$ gives more robust estimates.
- Higher $k$ corresponds to higher bias on negative events

Stochastic Gradient Descent

\mathcal{L} = \sum_{u \in V} \sum_{v \in N_R{u}} - \log(P(v|\textbf{z}_u))

How to we optimize (minimize) it?

Stochastic Gradient Descent: Instead of evaluating gradients over all examples, evaluate it for each individual training example.

Initialize $\textbf{z}_u$ at some randomized value for all nodes $u$ .

Iterate until convergence: $\mathcal{L}^{(u)} = \sum_{v \in N_R(u)} - \log (P(v|\textbf{z}_u)$
- Sample a node $u$ , for all $v$ calulate the gradient $\frac{\partial \mathcal{L}^{(u)}}{\partial \textbf{z}_v}$
- For all $v$ , update: $\textbf{z}_v \leftarrow \textbf{z}_v - \eta \frac{\partial \mathcal{L}^{(u)}}{\partial \textbf{z}_v}$

Node2vec Algorithm (Linear-time complexity + All 3 steps are individually parallelizable)

Compute edge transition probabilities:
1. For each edge $(s_1,w)$ we compute edge walk probabilities (based on $p,q$ ) of edge $(w;)$

Simulate $r$ random walks of length $l$ starting from each node $u$

Optimize the node2vec objective using Stochastic Gradient Descent

Embeddings Entire Graphs

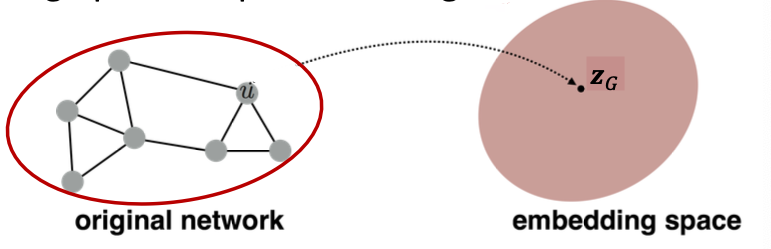
Goal: Want to embed a subgraph or an entire graph $G$ . Graph embedding: $\textbf{z}_G$ .

Approach 1 ( 简单但是有效奥)
- Run a standard graph embedding technique on the (sub)graph $G.$
- Then just sum (or average) the node embeddings in the (sub)graph $G.$
$\textbf{z}_G = \sum_{v \in G} \textbf{z}_v$

Approach 2
- Introduce a “virtual node” to represent the (sub)graph and run a standard graph embedding technique

Hierarchical Embeddings

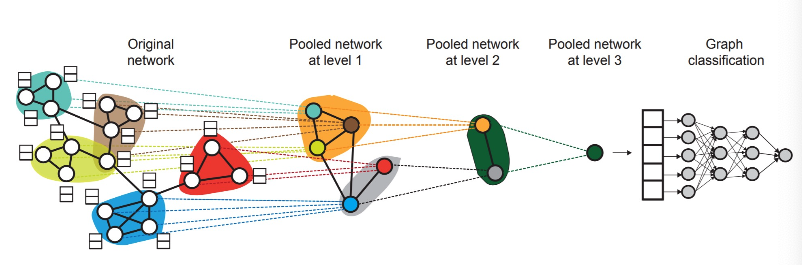
DiffPool: We can also hierarchically cluster nodes in graphs, and sum/average the node embeddings according to these clusters.

Matrix Factorization and Node Embeddings (矩阵分解和节点嵌入)

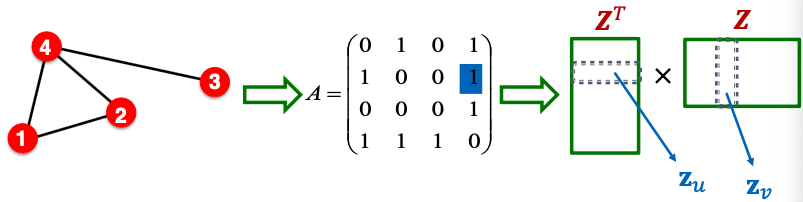
Connection to Matrix Factorization

Simplest node similarity: Node $u,v$ are similar if they are connected by an edge.

This means: $\textbf{z}^T_v \textbf{z}_u = A_{u,v}$ , which is the $(u,v)$ entry of the graph adjacency matrix $A.$

Therefore, $\textbf{Z}^T \textbf{Z} = A$

其他矩阵分解相关内容可见 (Applied Linear Algebra for Data Science Lecturenotes)

Random Walk - based Similarity

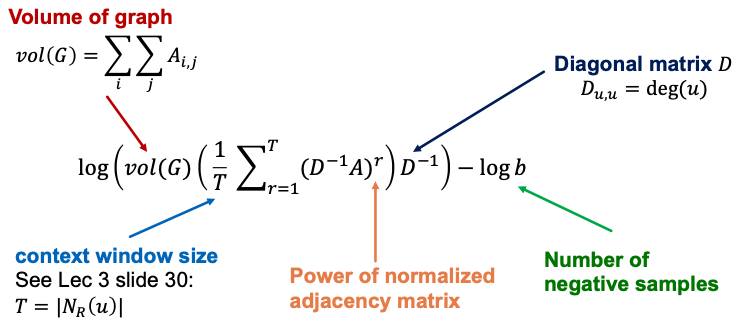
DeepWalk and node2vec have a more complex node similarity definition based on random walks

DeepWalk is equivalent to matrix factorization of the following complex matrix expression:
$\log (vol(G)(\frac{1}{T}\sum_{r=1}^T (D^{-1}A)^r)D^{-1}) - \log b$
Explanation of this equation

How to use Embeddings ? (怎么嵌入？)

Clustering/Community detection: Cluster points $\textbf{z}_i$ .

Node classification: Predict label of node $i$ based on $\textbf{z}_i$

Link Prediction: Predict edge $(i,j)$ based on $(\textbf{z}_i,\textbf{z}_j)$
- Where we can: concatenate, average, product, or take a difference between the embeddings:
  - Concatenate: $f(\textbf{z}_i,\textbf{z}_j) = g([\textbf{z}_i,\textbf{z}_j])$
  - Hadamard: $f(\textbf{z}_i,\textbf{z}_j) = g (\textbf{z}_i*\textbf{z}_j)$ per coordinate product
  - Sum/Average: $f(\textbf{z}_i,\textbf{z}_j) = g(\textbf{z}_i+\textbf{z}_j)$
  - Distance: $f(\textbf{z}_i,\textbf{z}_j) = g(||\textbf{z}_i-\textbf{z}_j||_2)$

Graph classification: Graph embedding $\textbf{z}_G$ via aggregating node embeddings or virtual-node. Predict label based on graph embedding $\textbf{z}_G.$