CS224W-Machine Learning with Graph-Theory

How powerful are GNNs?

Many GNN models have been proposed

What is the expressive power(ability to distinguish different graph structures) of these GNN models?

How to design a maximally expressive GNN model?

\text{A single GNN layer}

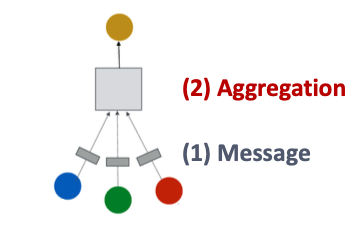
We focus on message passing GNNs:
- Message : each node computes a message
$\textbf{m}_u^{(l)} = \text{MSG}^{(l)}\left( \textbf{h}_u^{(l-1)},u\in \{N(v)\cup v\}\right)$
- Aggregation: aggregate messages from neighbors
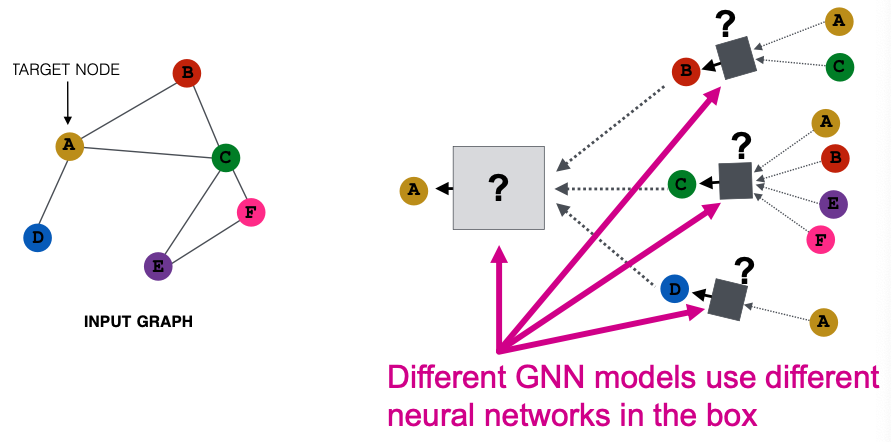
$\textbf{h}_v^{(l)} = \text{AGG}^{(l)} \left( \{ \textbf{m}_u^{(l)},u \in N(v)\},\textbf{m}_v^{(l)}\right)$

Many GNN Models
- Many GNN Models have been proposed:
  - GCN, GraphSAGE, GAT, Design Space etc.
- Example (GNN Model Example)
  - GCN (mean-pool) : Element-wise mean pooling + Linear + ReLUU non-linearity
  - GraphSAGE (max-pool) : MLP + element-wise max-pooling

Node Colors (节点染色)

We use node same/different colors to represent nodes with same/different features. (相同的颜色代表相同的特征或者说相同的意义，用颜色区分不同的feature)

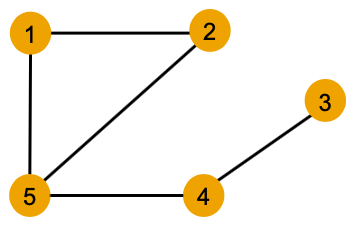
Local Neighborhood Structures

We specifically consider local neighborhood structures around each node in a graph.

Example: Nodes 1 and 5 have different neighborhood structures because they have different node degrees.

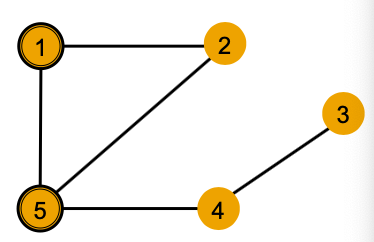
Example: Nodes 1 and 4 both have the same node degree of 2. However, they still have different neighborhood structures because their neighbors have different node degrees.

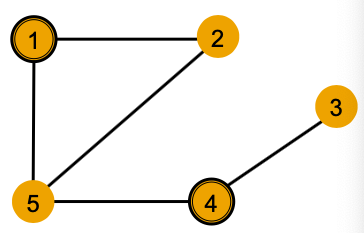
Example: Nodes 1 and 2 have the same neighborhood structure because they are symmetric within the graph.

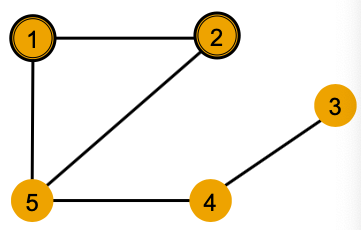
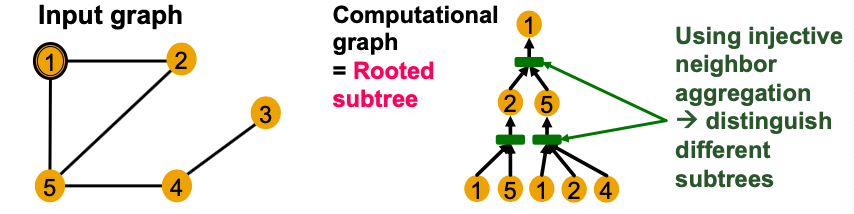
We need to understand how a GNN captures local neighborhood structures. (Computational Graph)

\text{Computational Graph}

In each layer, a GNN aggregate neighboring node embeddings.

A GNN generates node embeddings through a computational graph defined by the neighborhood.
- Example: Node 1’s computational graph (2-layer GNN)
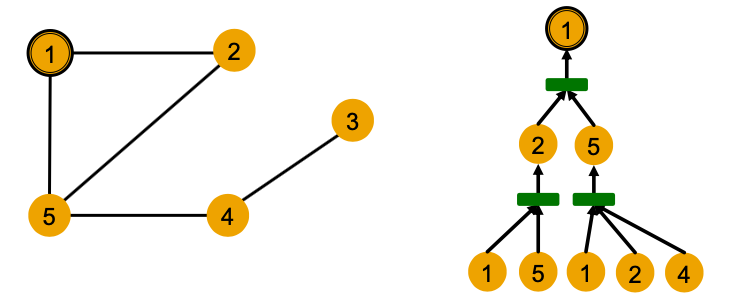
- Example: Nodes 1 and 2’s computational graphs. But GNN only sees node features (not IDs)

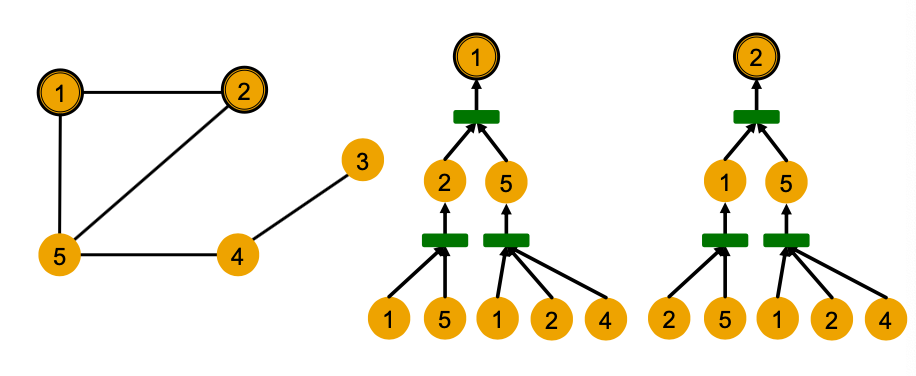
A GNN will generate the same embedding for nodes 1 and 2 because:
- Computational graphs are the same
- Node features (colors) are identical

GNN won’t be able to distinguish nodes 1 and 2

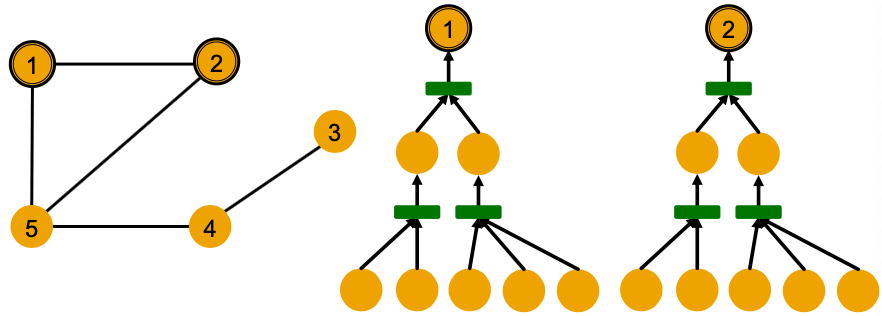
Note: GNN does not care about node ids, it just aggregates features vectors of different nodes.

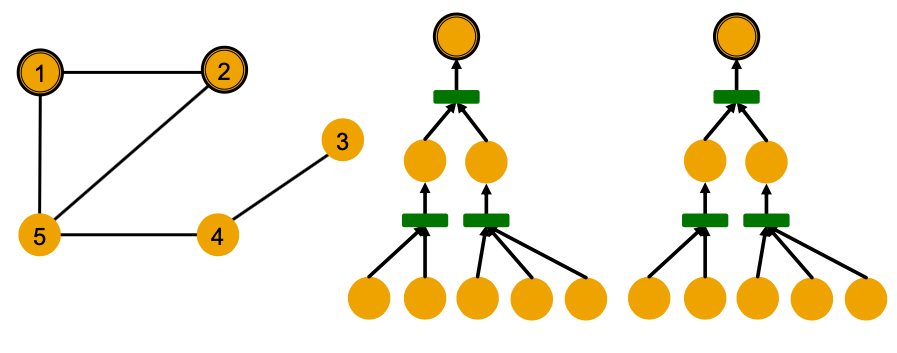
In general, different local neighborhoods define different computational graphs.

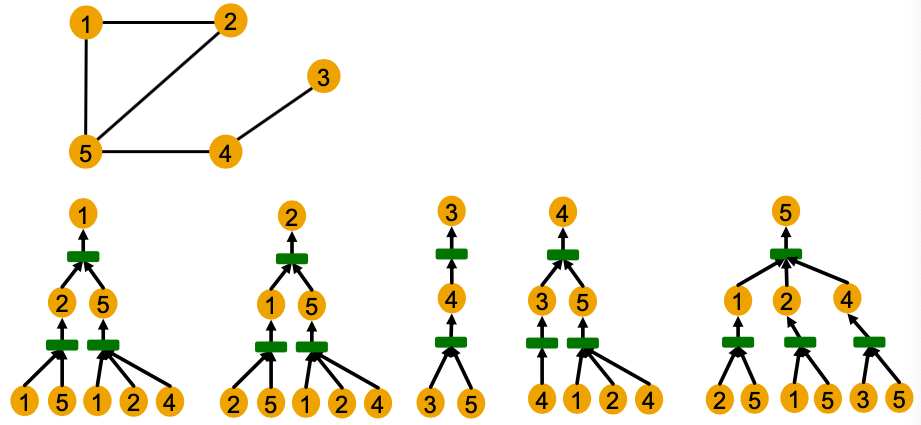
Computational graphs are identical to rooted subtree structures around each node.

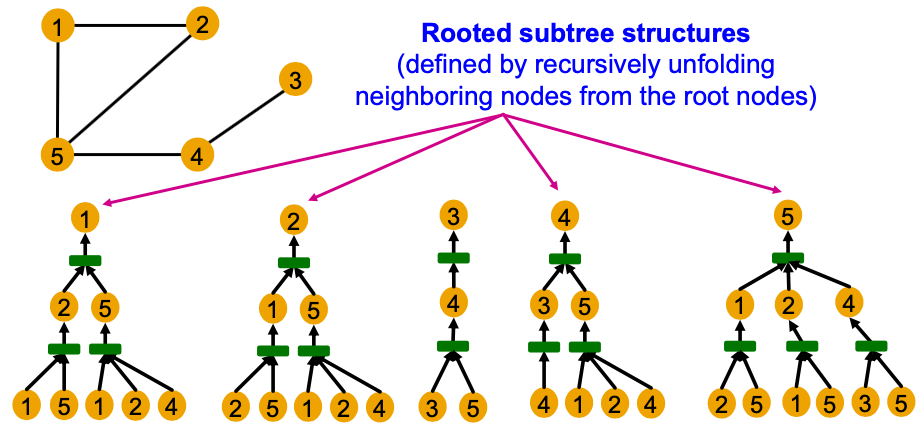
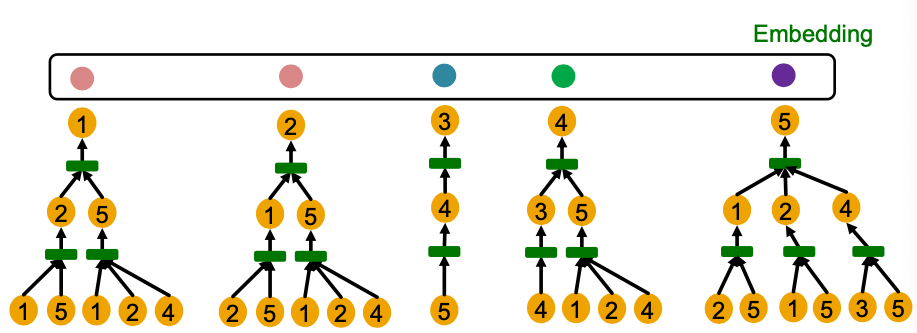
GNN’s node embeddings capture rooted subtree strucutrues.

Most expressive GNN maps different rooted subtrees into different node embeddings (represented by different colors).

\text{Recall: Injective Function}

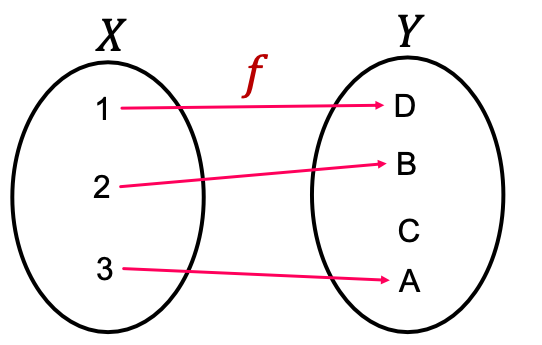
Function $f$ : $X \rightarrow Y$ is injective if it maps different elements into different outputs.

Intuition: $f$ retains all the information about input.

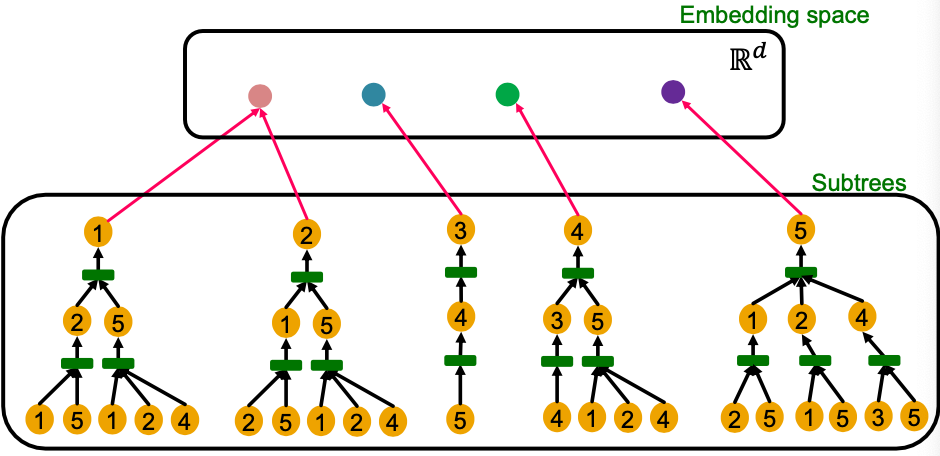
How Expressive is a GNN?

Most expressive GNN should map subtrees to the node embeddings injectively.

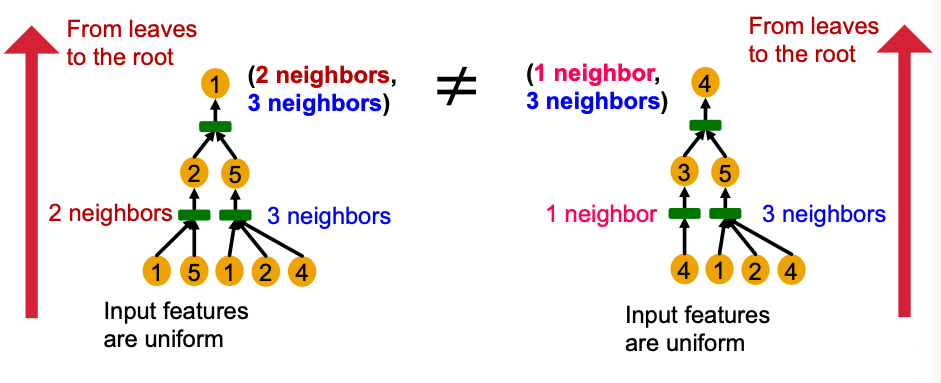
Key observation: Subtrees of the same depth can be recursively characterized from the leaf nodes to the root nodes.

If each step of GNN’s aggregation can fully retain the neighboring information, the generated node embeddings can distinguish different rooted subtrees.

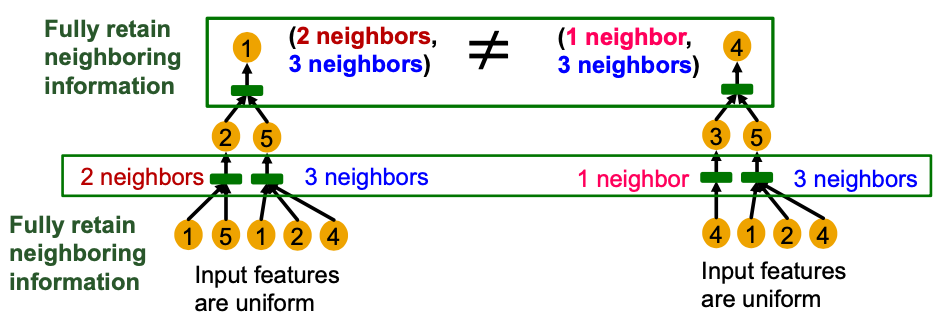
In other words, most expressive GNN would use an injective neighbor aggregation function at each step.
- Maps different neighbors to different embeddings.

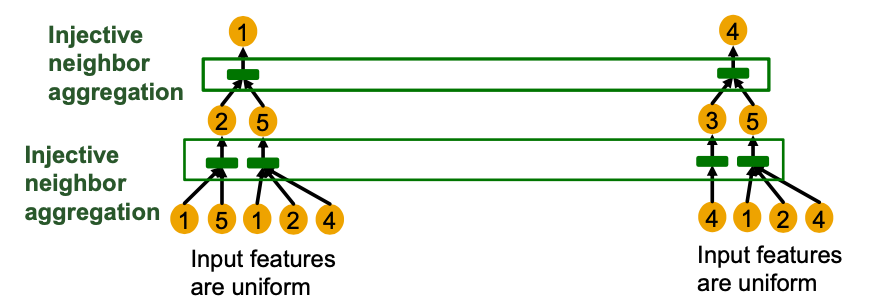
Summary so far
- To generate a node embedding, GNNs use a computational graph corresponding to a subtree rooted around each node.
- GNN can fully distingguish different subtree structures if every step of its neighbor aggregation is injective.

Expressive Power of GNNs

Key observation: Expressive power of GNNs can be characterized by that of neighbor aggregation functions they use.

A more expressive aggregation function leads to a more expressive GNN.

Injective aggregation function leads to the most expressive GNN

Theoretically analyze expressive power of aggregation functions

Observation: Neighbor aggregation can be abstracted as a function over a multi-set (a set with repeating elements)

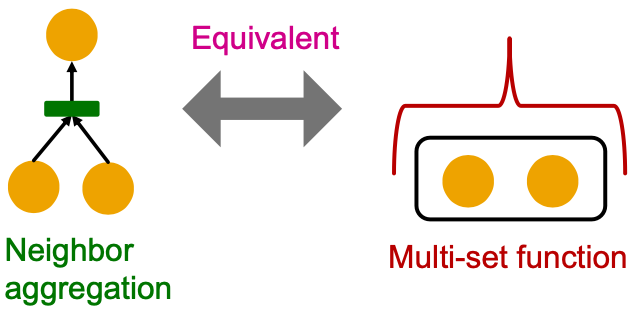
We analyze aggregation functions of two popular GNN models

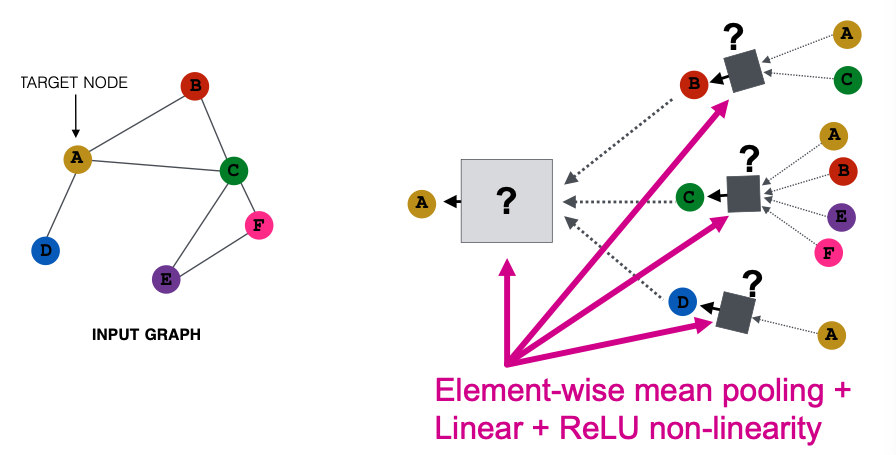
GCN (mean-pool)
- Uses element-wise mean pooling over neighboring node features
$\text{Mean} (\{ x_u\}_{u \in N(v)})$

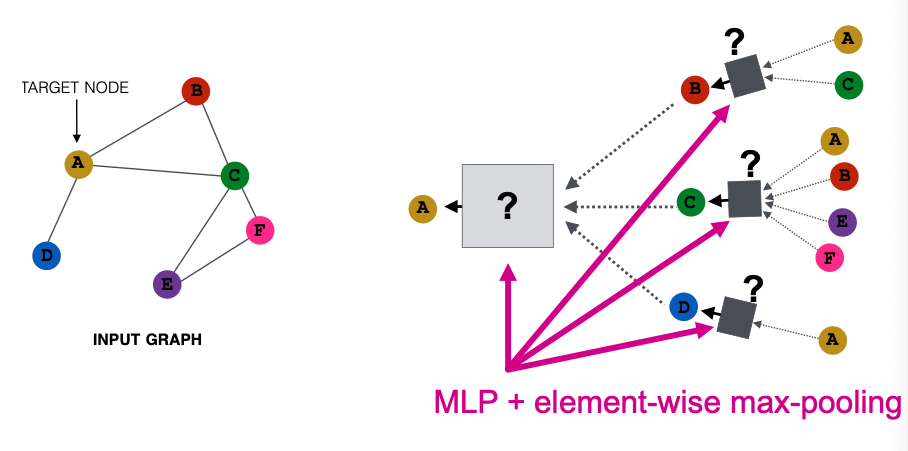
GraphSAGE (max-pool)
- Uses element-wise max pooling over neighboring node features
$\text{Max}(\{x_u\}_{u \in N(v)})$

Neighbor Aggregation: Case Study

GCN (mean-pool)
- Take element-wise mean, followed by linear function and ReLU activation, i.e., $max(0,x)$
- Theorem
  - GCN’s aggregation function cannot distinguish different multi-sets with the same color proportion.
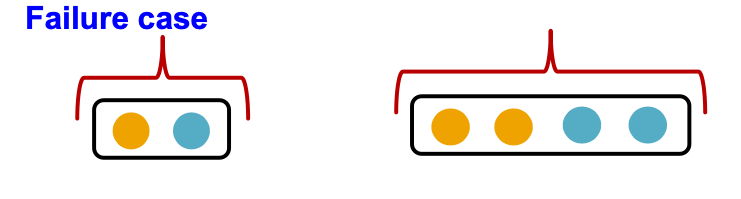
解释上面的理论，为什么会出现这个问题
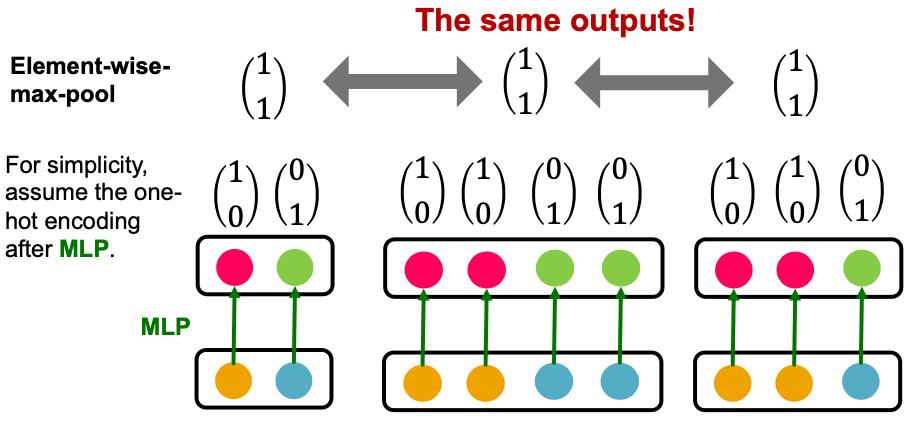
- For simplicity, we assume node features (colors) are represented by one-hot encoding.
  - Example: If there are two distinct colors:
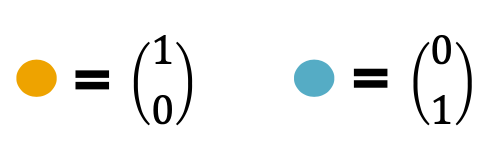
  - This assumption is sufficient to illustrate how GCN fails.
  - Failure case illustration

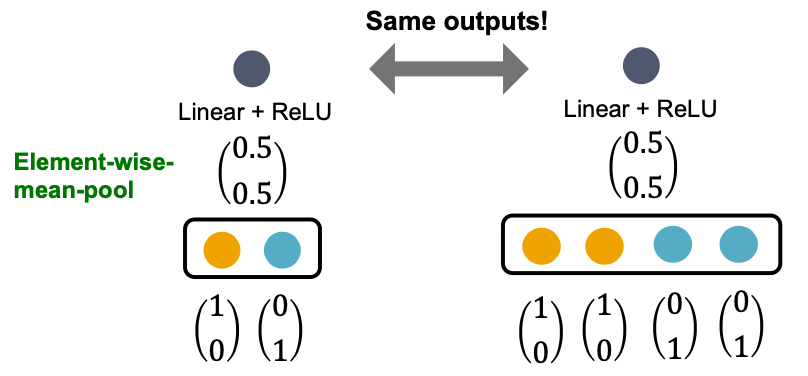
GraphSAGE (max-pool)
- Apply an MLP, then take element-wise max.
- Theorem
  - GraphSAGE’s aggregation function cannot distinguish different multi-sets with the same set of distinct colors.
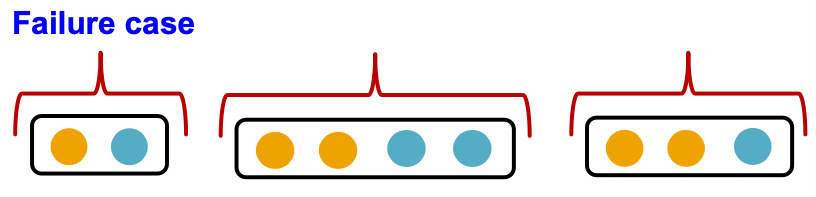
解释一下出现这种情况的原因
- Failure case illustration

Summary GCN 和 GraphSAGE的问题

Expressive power of GNNs can be characterized by that of the neighbor aggregation function

Neighbor aggregation is a function over multi-sets (sets with repeating elements)

GCN and GraphSAGE’s aggregation functions fail to distinguish some basic multi-sets; hence not injective.

Therefore, GCN and GraphSAGE are not maximally powerful GNNs.

Designing Most Expressive GNNs

Our goal: Design maximally powerful GNNs in the class of message-passing GNNs.

This can be achieved by designing injective neighbor aggregation function over multi-sets.

Here, we design a neural network that can model injective multiset function.

Injective Multi-Set Function

Theorem: Any injective multi-set function can be expressed as:

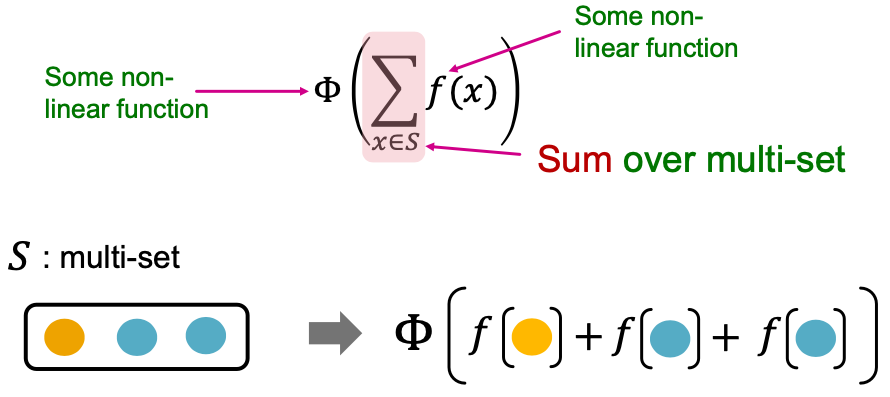
Proof Intuition: $f$ produces one-hot encodings of colors. Summation of the one-hot encodings retains all the information about the input multi-set.
$\Phi \left( \sum_{x \in S}f(x) \right)$

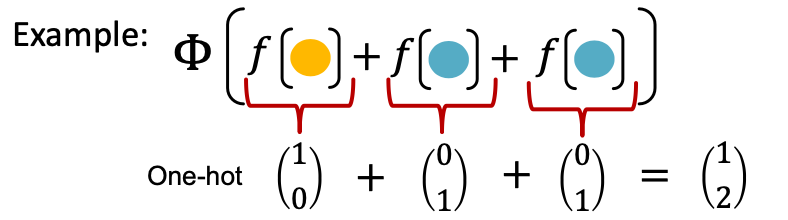
Universal Approximation Theorem

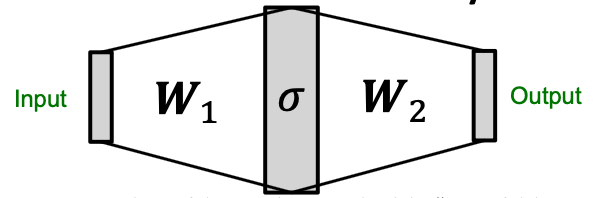
How to model $\Phi$ and $f$ in $\Phi (\sum_{x\in S} f(x))$ ?

We use a Multi-Layer Perceptron (MLP).

Theorem: Universal Approximation Theorem
- 1-hidden-layer MLP with sufficiently-large hidden dimensionality and appropriate non-linearity $\sigma(\cdot)$ (including ReLU and sigmoid) can approximate any continuous function to an arbitrary accuracy.

Injective Multi-Set Function

We have arrived at a neural network that can model any injective multi-set function.

\text{MLP}_{\Phi} \left( \sum_{x\in S} \text{MLP}_{f}(x)\right)

\text{Most Expressive GNN}

Graph Isomorphism Network (GIN)

Apply an MLP, element-wise sum, followed by another MLP.

\text{MLP}_{\Phi} \left( \sum_{x\in S} \text{MLP}_{f}(x)\right)

Theorem
- GIN’s neighbor aggregation function is injective.

No failure cases!

GIN is the most expressive GNN in the class of message-passing GNNs we have introduced!

We now describe the full model of GIN by relating it to WL graph kernel (traditional way of obtaining graph-level features).

Recall: Color refinement algorithm in WL kernel.

Given: A graph $G$ with a set of nodes $V$ .
- Assign an initial color $c^{(0)}(v)$ to each node $v$ .
- Iteratively refine node colors by
$c^{(k+1)}(v) = \text{HASH} \left( c^{(k)}(v),\{c^{(k)}(u)\}_{u \in N(v)}\right)$
where HASH maps different inputs to different colors.
- After $K$ steps of color refinement, $c^{(K)}(v)$ summarizes the structure of $K-hop$ neighborhood

\text{Color Refinement Algorithm}

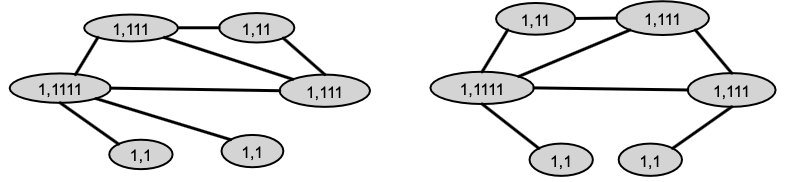
Example of color refinement given two graphs

Assign initial colors

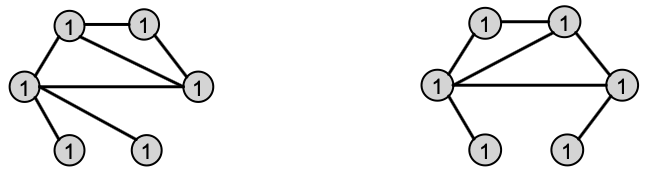
Aggregate neighboring colors

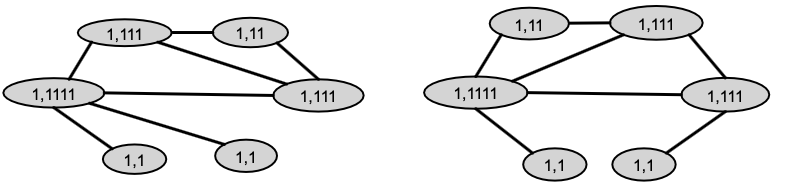
逗号后面1的个数就是这个节点相连接的节点（个数）

Aggregated colors

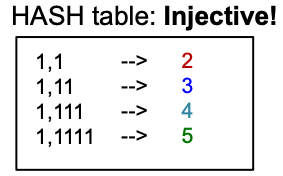
Injectively HASH the aggregated colors

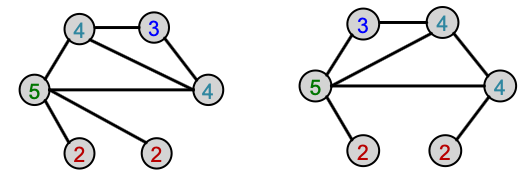
Process continues until a stable coloring is reached

Two graphs are considered isomorphic if they have the same set of colors.

\text{The Complete GIN Model}

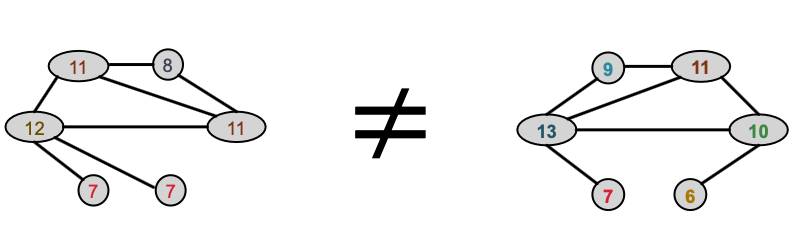
GIN uses a neural network to model the injective HASH function.

c^{(k+1)}(v) = \text{HASH} \left( c^{(k)}(v),\{c^{(k)}(u)\}_{u\in N(v)}\right)

Specifically, we will model the injective function over the tuple:
- $c^{(k)}(v)$ : Root node features
- $c^{(k)}(u)_{u \in N(v)}$ : Neighboring node colors

(c^{(k)}(v), \{c^{(k)}(u)\}_{u \in N(v)})

Theorem: Any injective function over the tuple
$(c^{(k)}(v), \{c^{(k)}(u)\}_{u \in N(v)})$

can be modeled as

\text{MLP}_{\Phi}\left((1+\epsilon) \cdot \text{MLP}_f (c^{(k)}(v)) + \sum_{u \in N(v)} \text{MLP}_f(c^{(k)}(u))\right)

where $\epsilon$ is a learnable scalar.

If input feature $c^{(0)}(v)$ is represented as one-hot, direct summation is injective.

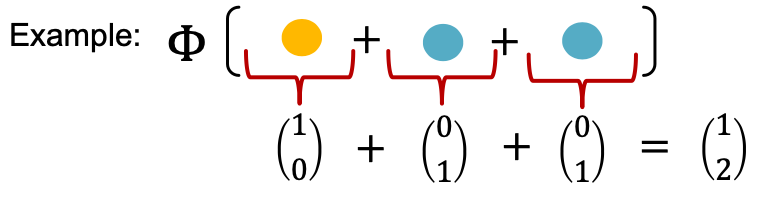
We only need $\Phi$ to ensure the injectivity.

GIN’s node embedding updates

Given: A graph $G$ with a set of nodes $V$ .
- Assign an initial vector $c^{(0)}(v)$ to each node $v$ .
- Iteratively update node vectors by
$c^{(k+1)}(v) = \text{GINConv}\left(\{c^{(k)}(v),\{c^{(k)}(u)\}_{u\in N(v)}\}\right)$
where GINConv maps different inputs to different embeddings.
- After $K$ steps of GIN iterations, $c^{(K)}(v)$ summarizes the structure of $K$ -hop neighborhood.

\text{GIN vs WL Graph Kernel}

GIN can be understood as differentiable neural version of the WL graph Kernel:

	Update target	Update function
WL Graph Kernel	Node colors (one-hot)	HASH
GIN	Node embeddings (low-dim vectors)	GINConv

Advantages of GIN over the WL graph kernel are:

Node embeddings are low-dimensional; hence, they can capture the fine-grained similarity of different nodes.

Parameters of the update function can be learned for the downstream tasks.

Because of the relation between GIN and the WL graph kernel, their expressive is exactly the same.

If two graphs can be distinguished by GIN, they can be also distinguished by the WL kernel, and vice versa.

How powerful is this?

WL kernel has been both theoretically and empirically shown to distinguish most of the real-world graphs.

Hence, GIN is also powerful enough to distinguish most of the real graphs

Improving GNNs’ Power

Can the expressive power of GNNs be improved?

There are basic graph structures that existing GNN framework cannot distinguish, such as difference in cycles.

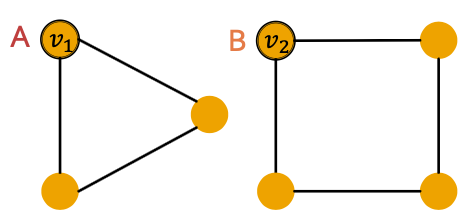
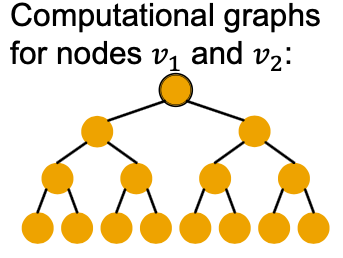
GNNs’ expressive power can be improved to resolve the above problem.