CS224W-Machine Learning with Graph-Heterogeneous

How to handle graphs with multiple nodes or edge types (a.k.a heterogeneous graphs)?

Goal: Learning with heterogeneous graphs

Relational GCNs

Heterogeneous Graph Transformer

Design space for heterogeneous GNNs

Motivation

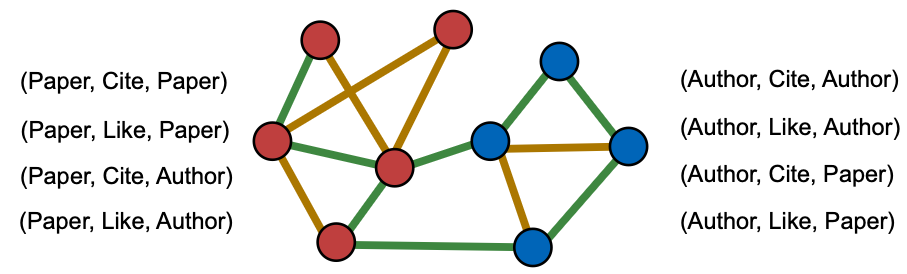
2 types of nodes:
- Node type A: Paper nodes
- Node type B: Author nodes

2 types of edges:
- Edge type A: Cite
- Edge type B: Like

2 types of nodes + 2 types of edges
- Relation types: (node_start, edge, node_end)
- We use relation type to describe an edge (as opposed to edge type)
- Relation type better captures the interaction between nodes and edges

\text{Heterogeneous Graphs}

A heterogeneous graph is defined as

G = (V,E,\tau,\phi)

Nodes with node types $v\in V$
- Node type for node $v: \tau(v)$

Edges with edge types $(u,v) \in E$ (An edge can be described as a pair of nodes)
- Edge type for edge $(u,v):\phi(u,v)$
- Relation type for edge $e$ is a tuple: $r(u,v) = (\tau(u),\phi(u,v),\tau(v))$

There are other definitions for heterogeneous graphs as well - describe graphs with node & edge types.

\text{Many Graphs are Heterogeneous Graphs}

Observation: We can also treat types of nodes and edges as features

Example: Add a one-hot indicator for nodes and edges
- Append feature $[1,0]$ to each “author node”; Append feature $[0,1]$ to each “paper node”
- Similarly, we can assign edge features to edges with different types.

Then, a heterogeneous graph reduces to a standard graph

When do we need a heterogeneous graph?

Case 1: Different node/edge types have different shapes of features
- An “author node” has 4-dim feature, a “paper node” has 5-dim feature

Case 2: We know different relation types represent different types of interactions
- (English, translate, French) and (English, translate, Chinese) require different models

Heterogeneous graph is a more expressive graph representation!

Captures different types of interactions between entities.

But it also comes with costs

More expensive (computation, storage)

More complex implementation

There are many ways to convert a heterogeneous graph to a standard graph(that is, a homogeneous graph(同构))

Classical GNN Layers: GCN

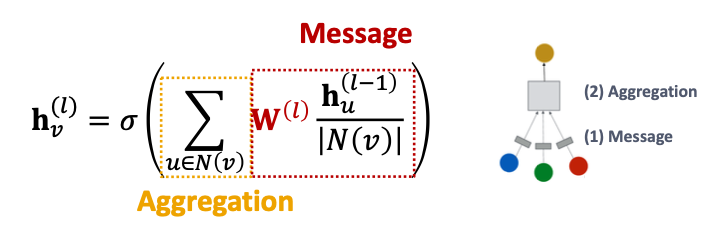
Graph Convolutional Networks (GCN)

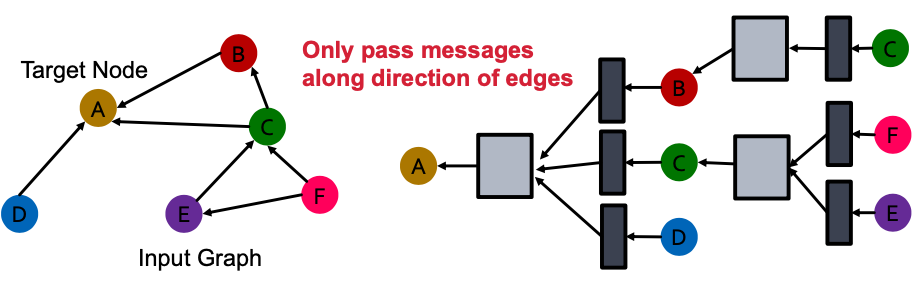
\textbf{h}_v^{(l)} = \sigma \left(\textbf{W}^{(l)} \sum_{u\in N(v)}\frac{\textbf{h}_u^{(l-1)}}{|N(v)|}\right)

How to write this as Message + Aggegation?

\text{Relational GCN}

We will extend GCN to handle heterogeneous graphs with multiple edge /relation types

We stat with a directed graph with one relation

How do we run GCN and update the representation of the target node A on this graph?

What is the graph has multiple relation types?

Use different neural network weights for different relation types.

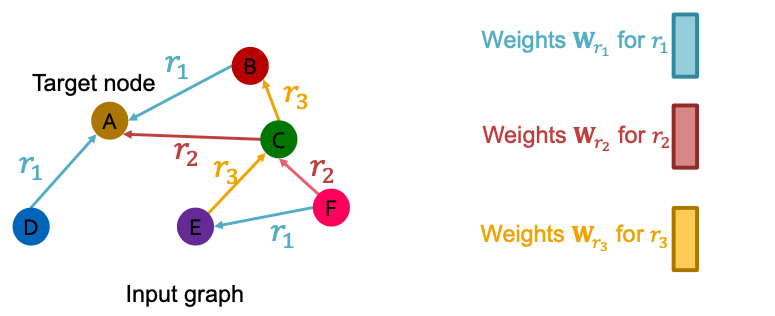
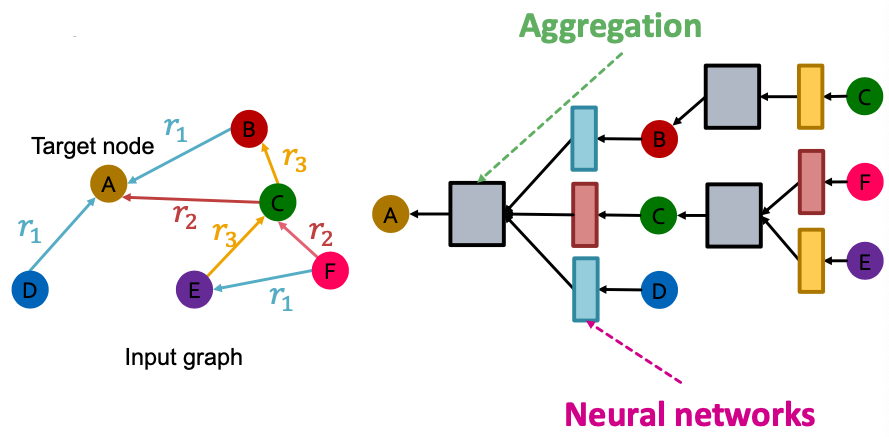
Introduce a set of neural networks for each relation type!

Relational GCN: Definition

Relational GCN(RGCN):

\textbf{h}_v^{(l+1)} = \sigma \left( \sum_{r\in R}\sum_{u\in N^r_u} \frac{1}{c_{v,r}}\textbf{W}^{(l)}_r \textbf{h}_u^{(l)}+\textbf{W}_0^{(l)}\textbf{h}_v^{(l)}\right)

How to write this as Message + Aggregation?

Normalized by node degree of the relation $c_{v,r} = |N^r_v|$

Message:
- Each neighbor of a given relation:
$\textbf{m}^{(l)}_{u,r} = \frac{1}{c_{v,r}} \textbf{W}^{(l)}_r \textbf{h}_u^{(l)}$
- Self-loop:
$\textbf{m}_v^{(l)} = \textbf{W}_0^{(l)} \textbf{h}_v^{(l)}$

Aggregation:
- Sum over messages from neighbors and self-loop, then apply activation
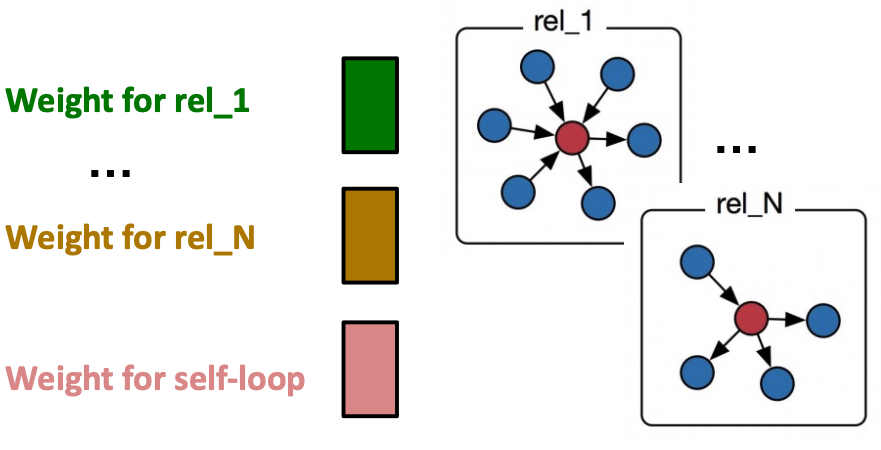
- $\textbf{h}_v^{(l+1)} = \sigma \left(Sum(\{\textbf{m}^{(l)}_{u,r},u\in N(v)\}\cup \{\textbf{m}_v^{(l)}\}) \right)$

RGCN: Scalability (可扩展性)

Each relation has $L$ matrices: $\textbf{W}_r^{(1)},\cdots,\textbf{W}_{r}^{(L)}$

The size of each $\textbf{W}_r^{(l)}$ is $d^{(l+1)} \times d^{(l)}$
- $d^{(l)}$ is the hidden dimension in layer $l$

Rapid growth of the number of parameters w.r.t number of relations! - Overfitting becomes an issue.

Two methods to regularize the weights $\textbf{W}_r^{(l)}$
- Use block diagonal matrices
  - Key insight: make the weights spare!
  - Use block diagonal matrices for $\textbf{W}_r$
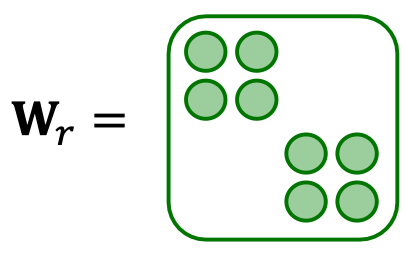
  - Limitation: only nearby neurons/dimensions can interact through $W$
  - If use $B$ low-dimensional matrices, then # param reduces form $d^{(l+1)} \times d^{(l)}$ to $B \times \frac{d^{(l+1)}}{B} \times \frac{d^{(l)}}{B}$
- Basis/Dictionary learning
  - Key insight: Share weights across different relations!
  - Represent the matrix of each relation as a linear combination of basis transformations $\textbf{W}_r = \sum_{b=1}^B a_{rb} \cdot \textbf{V}_b$ , where $\textbf{V}_b$ is shared across all relations
    - $\textbf{V}_b$ are the basis matrices
    - $a_{rb}$ is the importance weight of matrix $\textbf{V}_b$
  - Now each relation only needs to learn $\{a_{rb}\}_{b=1}^B$ , which is $B$ scalars

\text{Example: Entity/Node Classification}

Goal: Predict the label of a given node

RGCN uses the representation of the final layer:
- If we predict the class of node $A$ from $k$ classes
- Take the final layer (prediction head): $\textbf{h}_A ^{(L)} \in \mathbb{R}^k$ , each item in $\textbf{h}_A^{(L)}$ represents the probability of that class

\text{Example: Link Prediction}

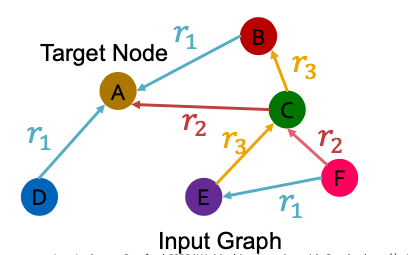
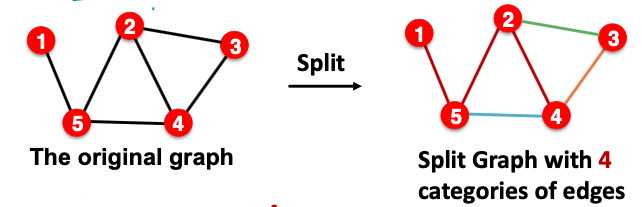
Link prediction split:
- Every edge also has a relation type, this is independent of the 4 categories.
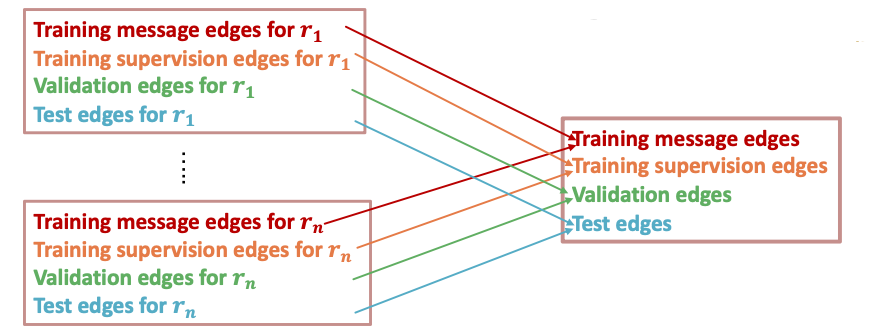
- In a heterogeneous graph, the homogeneous graphs formed by every single relation also have the 4 splits.

……更详细内容见其他。

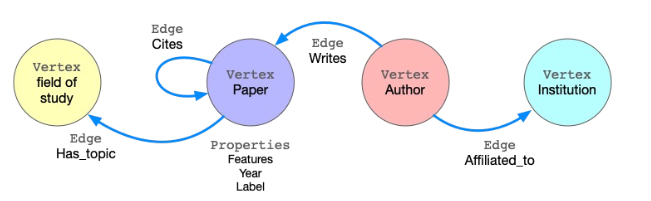
Benchmark for Heterogeneous Graphs

Summary of RGCN

Relational GCN, a graph neural network for heterogeneous graphs.

Can perform entity classification as well as link prediction tasks.

Ideas can easily be extended into RGCN (RGraphSAGE, RGAT, etc.)

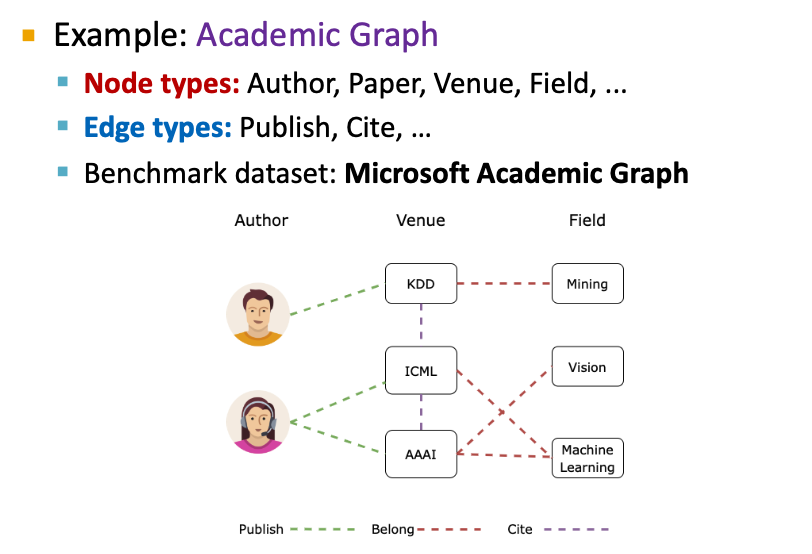
Benchmark: ogbn-mag from Microsoft Academic Graph, to predict paper venues

Heterogeneous Graph Transformer

Graph Attention Networks(GAT)

\textbf{h}_v^{(l)} = \sigma (\sum_{u\in N(v)}\alpha_{vu}\textbf{W}^{(l)} \textbf{h}_u^{(l-1)})

Not all node’s neighbors are equally important

Attention is inspired by cognitive attention.

The attention $\alpha_{vu}$ focuses on the important parts of the input data and fades out the rest.
- Idea: the NN should devote more computing power on that small but important part of the data.

Heterogeneous Graph Transformer

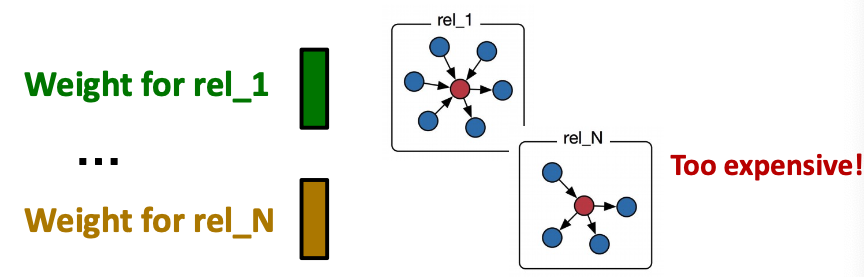
Motivation: GAT is unable to represent different node & different edge types.

Introduce a set of neural networks for each relation type is too expensive for attention
- Recall: relation describes (node_s, edge, node_e)

Basics: Attention in Transformer

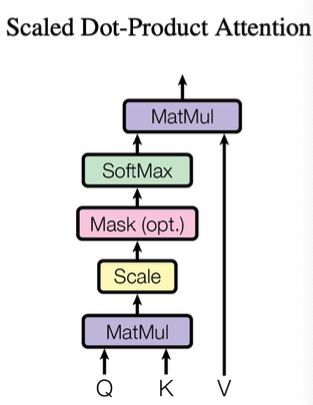
HGT uses Scaled Dot-Product Attention (proposed in Transformer)

\text{Attention}(Q,K,V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V

Query: $Q$ , key: $K$ , Value: $V$
- $Q,K,V$ have shape (batch_size, dim)

How do we obtain $Q,K,V$ ?

Apply Linear layer to the input
- $Q = Q\_Linear (X)$
- $K = K\_Linear(X)$
- $V=V\_Linear(X)$

Heterogeneous Mutual Attention

Recall: Applying GAT to a homogeneous graph

$\textbf{H}^{(l)}$ is the $l$ -th layer representation:

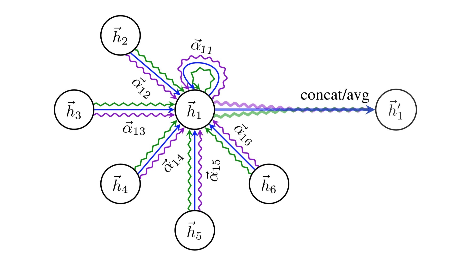
H^l[t] \leftarrow \text{Aggregate}_{\forall s \in N(t), \forall e\in E(s,t)}(Attention(s,t)\cdot Message(s))

Innovation: Decompose heterogeneous attention to Node- and edge-type dependent attention mechanism
- 3 node weight matrices, 2 edge weight matrices
- Without decomposition: $3\times2\times3=18$ relation types $\rightarrow$ $18$ weight matrices (suppose all relation types exist)

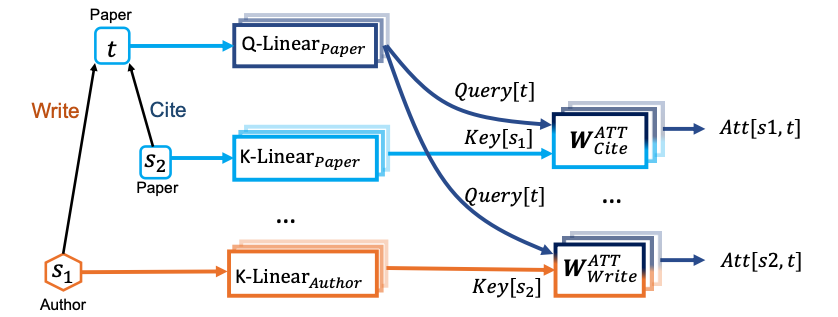
Heterogeneous Mutual Attention:

\begin{align*} ATT-head^i(s,e,t) &= (K^i(s)W^{ATT}_{\phi(e)}Q^{i}(t)^T) \\ K^i(s) &=K-Linear^i_{\tau(s)}(H^{(l-1)}[s])\\ Q^i(t) &= Q-Linear^i_{\tau(t)}(H^{(l-1)}[t]) \end{align*}

Each relation $(T(s),R(e),T(t))$ has a distinct set of projection weights
- $T(s)$ : type of node $s$ , $R(e)$ : type of edge $e$
- $T(s)$ & $T(t)$ parameterize $K\_Linear_{T(s)}$ & $Q\_Linear_{T(t)}$ , which further return Key and Query vectors $K(s)$ & $Q(t)$
- Edge type $R(e)$ directly parameterizes $W_{R(e)}$

A full HGT layer

\widetilde{H}^{(l)}[t] = \oplus_{\forall s \in N(t)}(\textbf{Attention}_{HGT}(s,e,t)\cdot \textbf{Message}_{HGT}(s,e,t))

Similarly, HGT decomposes weights with node & edge types in the message computation

\textbf{Message}_{HGT}(s,e,t) = ||_{i \in [1,h]} \ MSG-head^i(s,e,t)

MSG-head^i(s,e,t) = M-Linear^i_{\tau(s)} (H^{(l-1)}[s])W^{MSG}_{\phi(e)}

$M-Linear^i_{\tau(s)}$ : Weights for each node type

$W^{MSG}_{\phi(e)}$ : Weights for each edge type

\text{Design Space of Heterogenous GNNs}

Heterogeneous message computation

Message function
$\textbf{m}_u^{(l)} = MSG_r^{(l)} (\textbf{h}_u^{(l-1)})$
- Observation: A node could receive multiple types of messages.
$Num\ of \ message \ type = Num \ of \ relation \ type$
- Idea: Create a different message function for each relation type
  - $\textbf{m}_u^{(l)} = MSG_r^{(l-1)}(\textbf{h}_u^{(l-1)})$ , $r = (u,e,v)$ is the relation type between node $u$ that sends the message, edge type $e$ , and node $v$ that receive the message
- Example : A Linear layer: $\textbf{m}_u^{(l)} = \textbf{W}_r^{(l)}\textbf{h}_u^{(l-1)}$

Heterogeneous Aggregation

Heterogeneous Aggregation
- Observation: Each node could receive multiple types of message from its neighbors, and multiple neighbors may belong to each message type.
- Idea: We can define a 2-stage message passing
  - $\textbf{h}_v^{(l)} = \text{AGG}_{all}^{(l)} (\text{AGG}_r^{(l)}(\{\textbf{m}_u^{(l)},u\in N_r(v)\}))$
  - Given all the messages sent to a node
  - Within each message type, aggregation the messages that belongs to the edge typee with $\text{AGG}_r^{(l)}$
  - Aggregate across the edge types with $\text{AGG}_{all}^{(l)}$
- Example: $\textbf{h}_v^{(l)} = \text{Concat}(\text{SUm}(\{\textbf{m}_u^{(l)},u\in N_r(v)\}))$

Heterogeneous GNN Layers

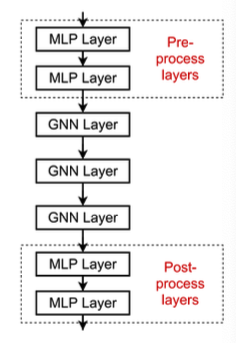
Heterogeneous pre/post-process layers:
- MLP layers with respect to each node type
  - Since the output of GNN are node embeddings
- $\textbf{h}_v^{(l)} = \text{MLP}_{T(v)} (\textbf{h}_v^{(l)})$
  - $T(v)$ is the type of node $v$

Other successful GNN designs are also encouraged for heterogeneous GNNs: Skip connections, batch/layer normalization, …

Heterogeneous Graph Manipulation

Graph Frature manipulation
- 2 Common options: compute graph statistics (e.g., node degree) within each relation type, or across the full graph (ignoring the relation types)

Graph Structure manipulation
- Neighbor and subgraph sampling are also common for heterogeneous graphs.
- 2 Common options: sampling within each relation type (ensure neighbors from each type are covered), or sample across the full graph.

Heterogeneous Prediction Heads

Node-level prediction

\hat{\textbf{y}}_v = \text{Head}_{node,T(v)}(\textbf{h}_v^{(L)}) = \textbf{W}_{T(v)}^{(H)}\textbf{h}_v^{(L)}

Edge-level prediction

\hat{\textbf{y}}_{uv} = \text{Head}_{edge,r} (\textbf{h}_u^{(L)},\textbf{h}_v^{(L)}) = \text{Linear}_r (\text{Conact}(\textbf{h}_u^{(L)}, \textbf{h}_v^{(L)}))

Graph-level prediction

\hat{\textbf{y}}_G = \text{AGG}(\text{Head}_{graph,i}(\{\textbf{h}_v^{(L)}\in \mathbb{R}^d,\forall T(v)=i\}))