CS224W-Machine Learning with Graph-Reasoning over Knowledge Graphs

Goal: How to perform multi-hop reasoning over KGs?

Can we do multi-hop reasoning, i.e., answer complex queries on an incomplete, massive KG?

One-hop Queries
- Example: What adverse event is caused by Fulvestrant? (e: Fulvestrant, (r:Causes))

Path Queries
- Example: What protein is associated with the adverse event caused by Fulvestrant? (e: Fulverstrant, (r: Causes, r: Assoc))

Conjunctive Queries
- Example: What is the drug that treats breast cancer and caused headache? ((e: BreastCancer,(r: TreatedBy)),(e: Migraine, (r: CausedBy)))

Predictive One-hop Queries

We can formulate knowledge graph completion problems as answering one-hop queries.

KG completion: Is link $(h,r,t)$ in the KG?

One-hop query: Is $t$ an answer to query $(h,r)$ ?
- For example: What side effects are caused by drug Fulvestrant?

Path Queries

Generalize one-hop queries to path queries by adding more relations on the path.

An $n$ -hop path query $q$ can be represented by
- $v_a$ is an “anchor” entity.
- Let answers to $q$ in graph $G$ be denoted by $\mathbb{[q]}_G$ .

q = (v_a,(r_1,\cdots,r_n))

Query Plan of $q:$ (Query plan of path queries is a chain.)

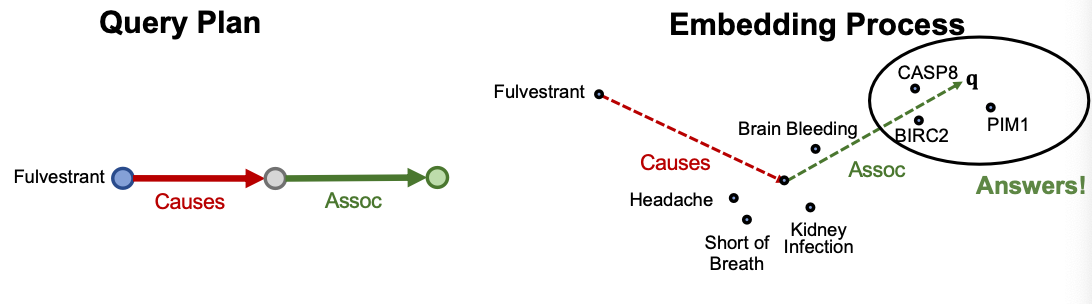
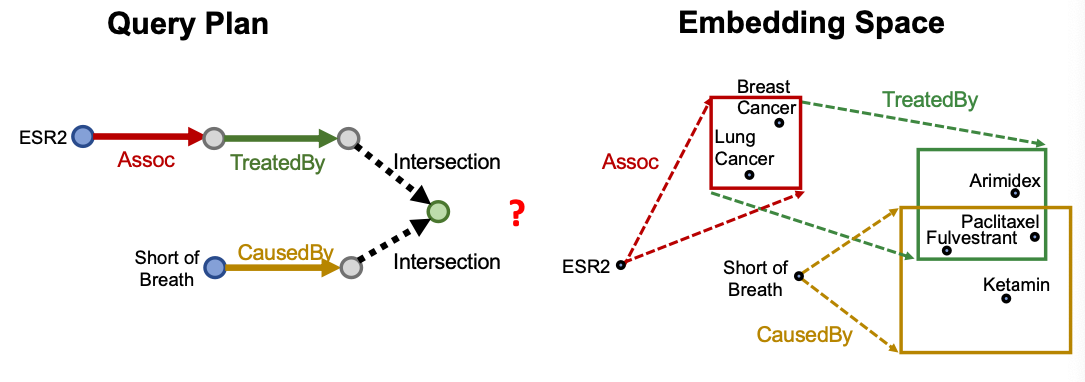
Question: “What proteins are associated with adverse events caused by Fulvestrant?”

$v_a$ is $e:$ Fulvestrant

$(r_1,r_2)$ is (r:Causes, r:Assoc)

Query: (e:Fulvestrant, (r:Causes,r:Assoc))

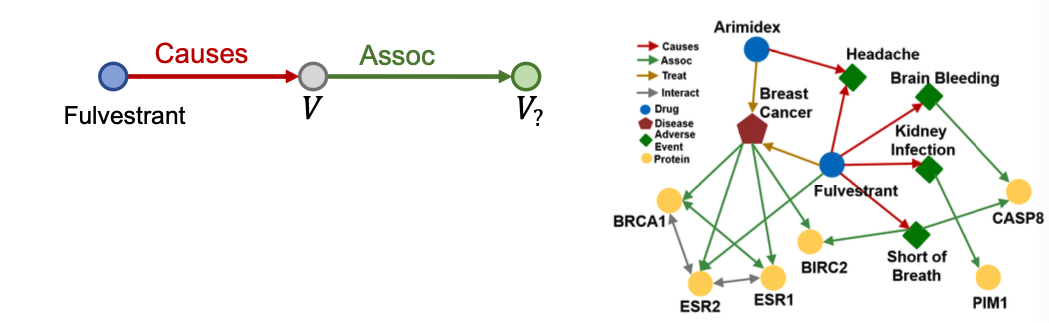
Traversing KG (遍历)

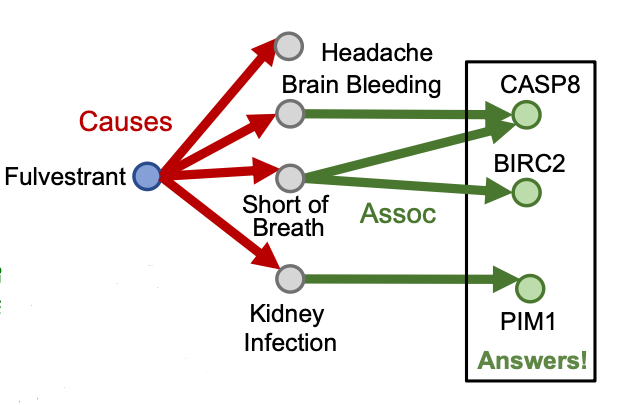
Start from the nodes {”Brain Bleeding”, ”Short of Breath”, ”Kidney Infection”, ”Headache”} and traverse the KG by the relation “Assoc”, we reach entities {”CASP8”, “BIRC2”, ”PIM1”}. These are the answers.

KGs are incomplete and unknown: Many relations between entities are missing or are incomplete

Due to KG incompleteness, one is not able to identify all the answer entities.

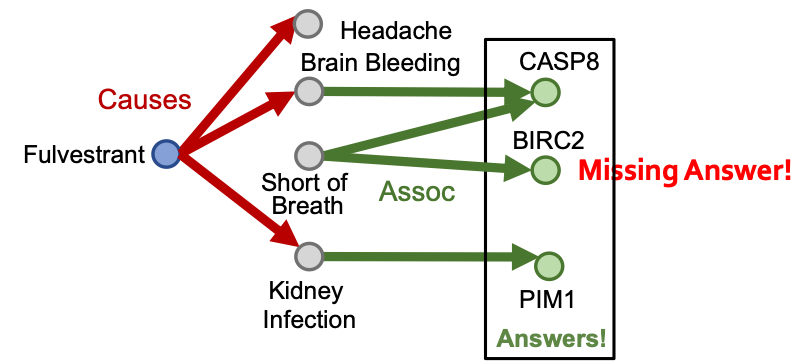
Can we first do KG completion and then traverse the completed (probabilistic) KG?

No! The “completed” KG is a dense graph!
- Most $(h,r,t)$ triples (edge on KG) will have some non-zero probability.

Time complexity of traversing a dense KG is exponential as a function of the path length $L:O(d^L_{max})$

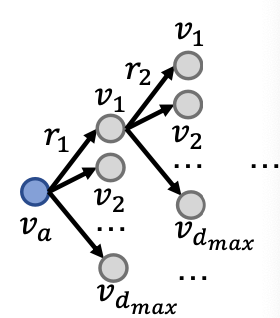
Given entity embeddings, how do we answer an arbitrary query?

Path queries: Using a generalization of TransE

Conjunctive queries: Using Query2Box

And-Or Queries: Using Query2Box and query rewriting

How do we train the embeddings?

The process of determining entity and relation embeddings which allow us to embed a query.

Answering Predictive Queries on Knowledge Graphs

General Idea

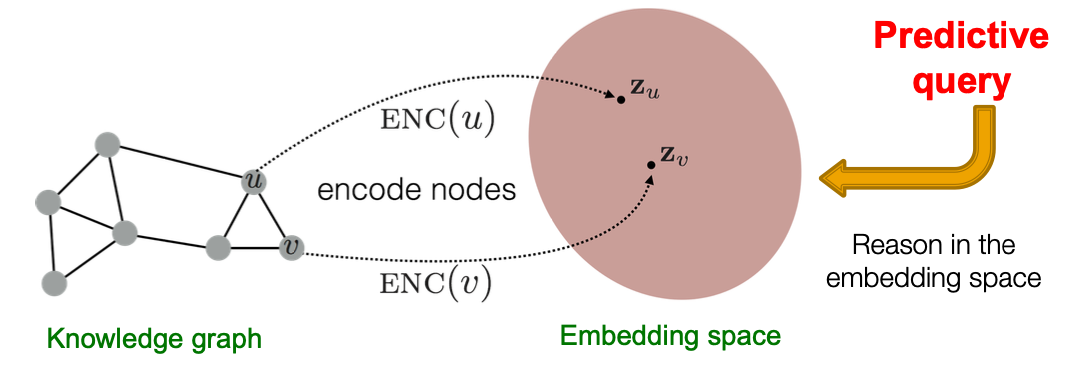
Map queries into embedding space. Learn to reason in that space.

Embed query into a single point in the Euclidean space: answer nodes are close to the query.

Query2Box: Embed query into a hyper-rectangle (Box) in the Euclidean space: answer nodes are enclosed in the box.

Idea: Traversing KG in Vector Space

Key idea: Embed queries!
- Generalize TransE to multi-hop reasoning.
Given a path query $q = (v_a,(r_1,\cdots,r_n))$ ,
- The embedding process only involves vector addition, independent of #entities in the KG!
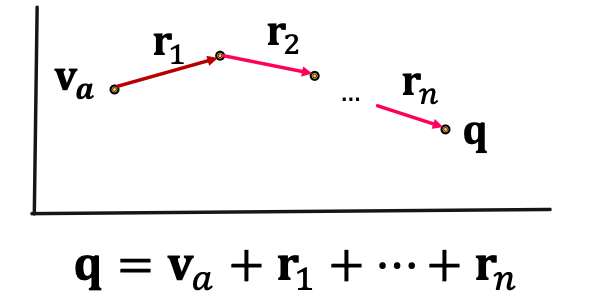
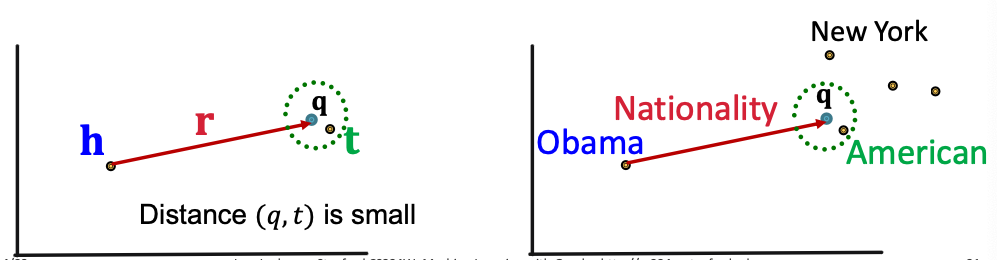
- Recap: TransE: Translate $h$ to $t$ using $r$ with score function $f_r(h,t) = - ||h+r-t||$
- Another way to interpret this is that:
  - Query embedding: $q=h+r$
  - Goal: query embedding $q$ is close to the answer embedding $t$
  $f_q(t) = -|| q-t||$

Embed path queries in vector space.

Question: “What proteins are associated with adverse events caused by Fulvestrant?”

Query: (e: Fulvestrant, (r:Causes, r:Assoc))

Follow the query plan:

We can train TransE to optimize knowledge graph completion objective (Lecture 11: GNNs for recommenders)

Since TransE can naturally handle compositional relations, it can handle path queries by translating in the latent space for multiple hops using addition of relation embeddings.

For DistMult / ComplEx, since they cannot handle compositional relations, they cannot be easily extended to handle path queries.

Can we answer more complex queries with logic conjunction operation?

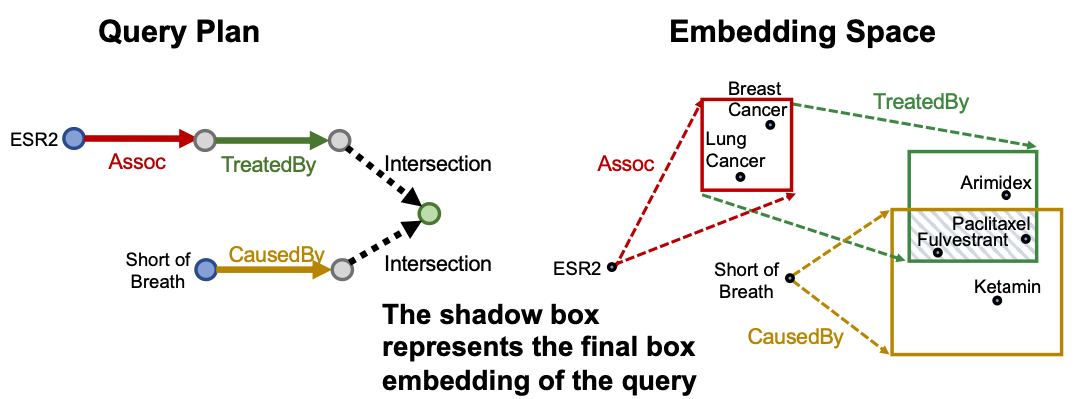
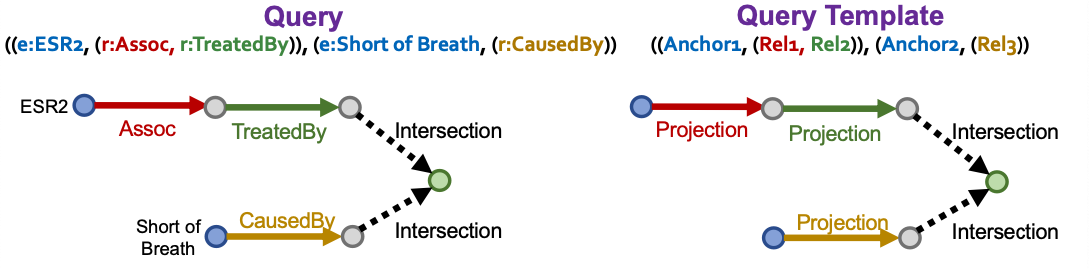
Conjunctive Queries: “What are drugs that cause Short of Breath and treat diseases associated with protein ESR2?” ((e:ESR2,(r:Assoc,r:TreatedBy)),(e:Short of Breath,(r:CausedBy)))

Question: Each intermediate node represents a set of entities, how do we represent it? How do we define the intersection operation in the latent space?

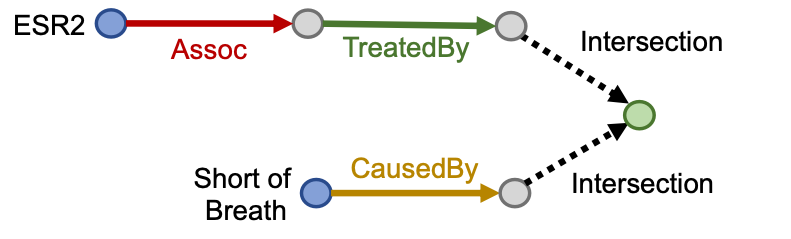
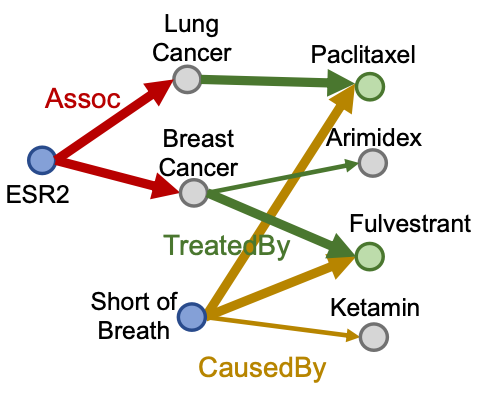
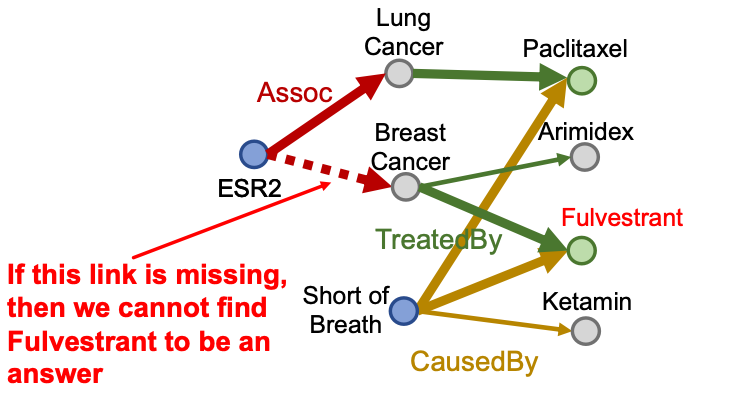
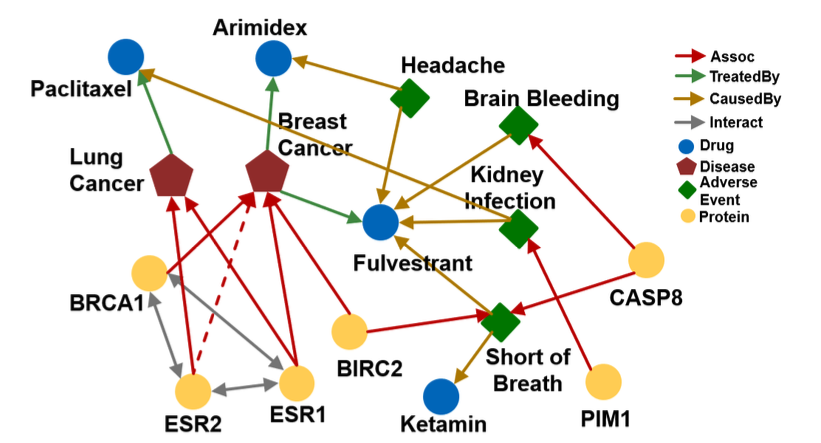
How can we use embeddings to implicitly impute the missing (ESR2, Assoc, Breast Cancer)?

ESR2 interacts with both BRCA1 and ESR1. Both proteins are associated with breast cancer.

Query2Box: Reasoning over KGs Using Box Embeddings

How can we answer more complex queries with logical conjunction operation?

Query plan:

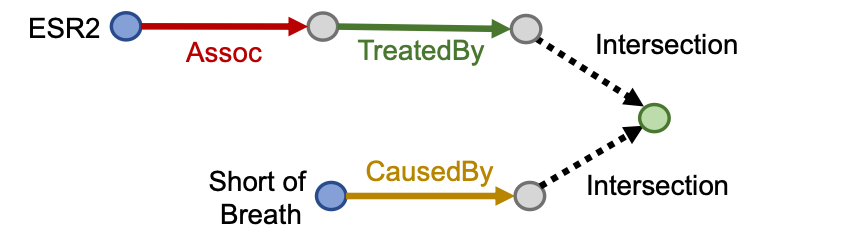
Each intermediate node represents a set of entities; how do we represent it?

How do we define the intersection operation in the latent space?

Box Embeddings

Embed queries with hyper-rectangles (boxes)
$q = (Center(q),Offset(q))$

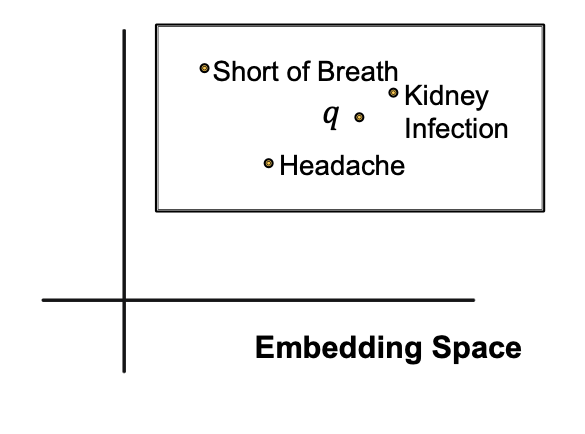
For example, we can embed the adverse events of Fulvestrant with a box that enclose all the answer entities.

Key Insight: Intersection

Intersection of boxes is well-defined!

When we traverse the KG to find the answer, each step produces a set of reachable entities.

How can we better model these sets?
- Boxes are a powerful abstraction, as we can project the center and control the offset to model the set of entities enclosed in the box.

Embed with Box Embedding

Things to figure out:

Entities embeddings (# params: $d|V|$ )
- Entities are seen as zero-volume boxes

Relation embeddings (# params: $2d|R|$ )
- Each relation takes a box and produces a new box

Intersection operator $f:$
- New operator, inputs are boxes and output is a box.
- Intuitively models intersection of boxes.

Notation: $d$ out degree, $|V|:$ # entities, $|R|$ : # relations

Projection Operator

Intuition:
- Take the current box as input and use the relation embedding to project and expand the box!

$\mathcal{P}$ : Box $\times$ Relation $\longrightarrow$ Box

\begin{align*} Cen(q') &= Cen(q) + Cen(r) \\ Off(q') &= Off(q) + Off(r) \end{align*}

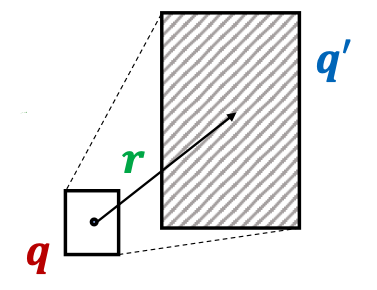
“x” (cross) means the projection operator is a relation from any box and relation to a new box

How do we take intersection of boxes?

Geometric Intersection Operator

Take multiple boxes as input and produce the intersection box

Intuition:
- The center of the new box should be “close” to the centers of the input boxes
- The offset (box size) should shrink (since the size of intersected set is smaller than the size of all the input set)

$\mathcal{J}$ : $\text{Box} \times \cdots \times \text{Box} \longrightarrow \text{Box}$

Cen(q_{inter}) = \sum_i w_i \odot Cen(q_i) \\ w_i = \frac{exp(f_{cen}(Cen(q_i)))}{\sum_j exp(f_{cen}(Cen(q_j)))}

$Cen(q_i) \in \mathbb{R}^d, w_i \in \mathbb{R}^d$

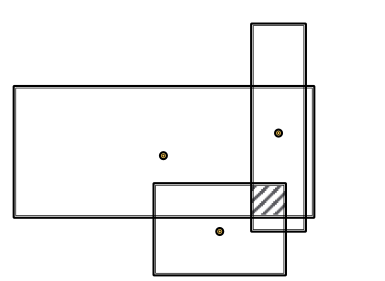
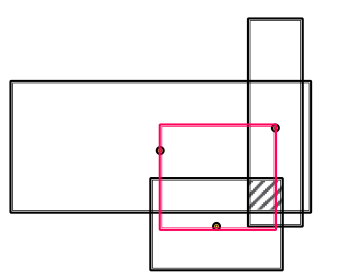
Intuition: The center should be in the red region!

Implementation: The center is a weighted sum of the input box centers

$w_i \in \mathbb{R}^d$ is calculated by a neural network $f_{cen}$ (with trainabnle weights)

$w_i$ represents a “self-attention” score for the center of each input $Cen(q_i)$

Off(q_{inter}) = min (Off(q_1),\cdots,Off(q_n)) \odot \sigma (f_{off}(Off(q_1),\cdots,Off(q_n)))

Intuition: The offset should be smaller than the offset of the input box

Implementation: We first take minimum of the offset of the input box, and then we make the model more expressive by introducing a new function $f_{off}$ to extract the representation of the input boxes with a sigmoid function to guarantee shrinking.

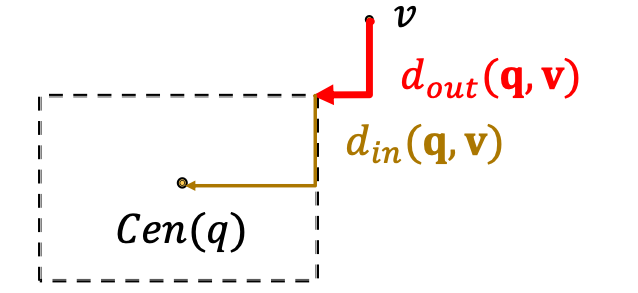
Entity-to-Box Distance

How do we define the score function $f_q(v)$ (negative distance)?

( $f_q(v)$ captures inverse distance of a node $v$ as answer to $q$ )

Given a query box $q$ and entity embedding (box) $v$ ,

d_{box}(q,v) = d_{out}(q,v) + \alpha \cdot d_{in}(q,v)

where $0< \alpha <1$ .

Intuition: if the point is enclosed in the box, the distance should be down-weighted.

$f_q(v) = - d_{box }(q,v)$

Extending to Union Operation

Can we embed complex queries with union?

E.g.: “What drug can treat breast cancer or lung cancer?”

Conjunction queries + disjunction is called Existential Positive First-order (EPFO) queries. We will refer to them as AND-OR queries.

Can we also design a disjunction operator and embed AND-OR queries in low-dimensional vector space?
- No! Intuition: Allowing union over arbitrary queries requires high-dimensional embeddings!

Example:

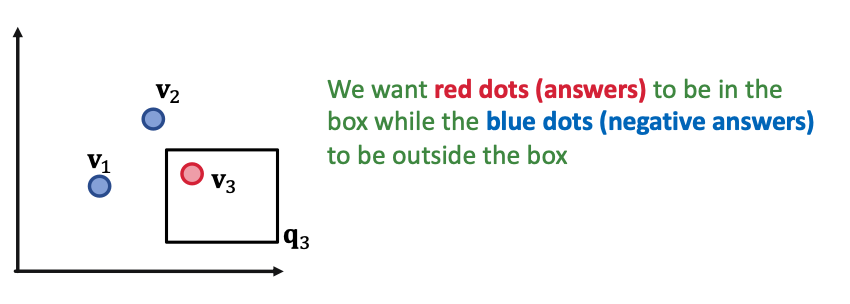
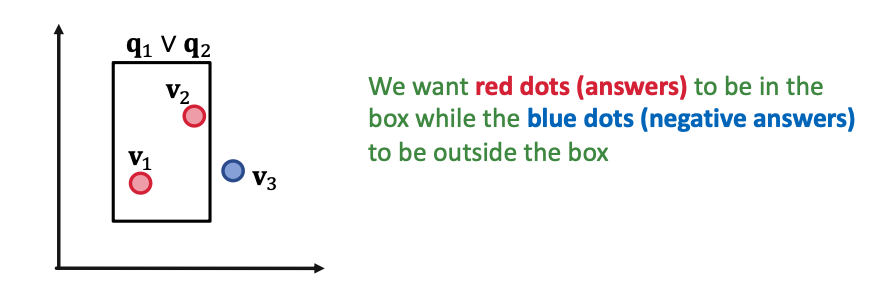
Given 3 queries $q_1,q_2,q_3$ , with answer sets:

$[q_1] = \{v_1\}, [q_2] = \{ v_2\},[q_3] = \{v_3\}$

If we allow union operation, can we embed them in two-dimensional plane?

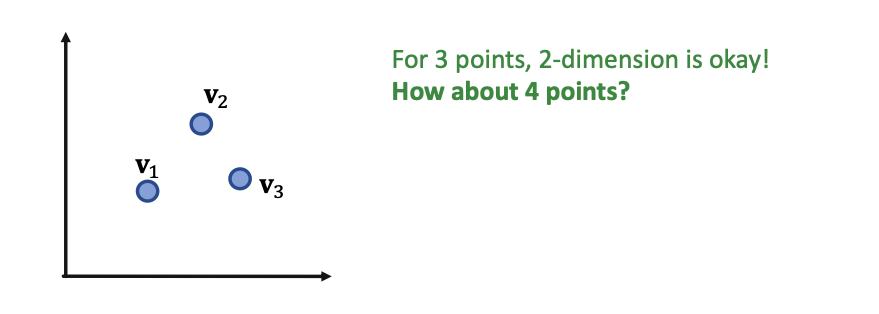
Example 2:

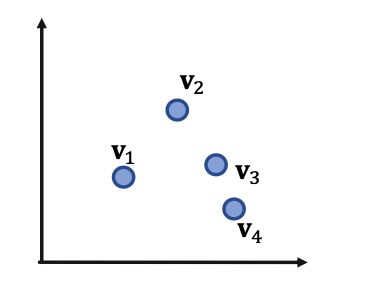
Given 4 queries $q_1,q_2,q_3,q_4$ with answers:

$[q_1] = \{v_1\}, [q_2] = \{ v_2\},[q_3] = \{v_3\}, [q_4] = \{v_4\}$

If we allow union operation, can we embed them in two-dimensional plane?

Can we embed AND-OR queries in low-dimensional vector space?

Conclusion: Given any $M$ conjunctive queries $q_1,\cdots,q_M$ with non-overlapping answers, we need dimensionality of $\Theta(M)$ to handle all OR queries.
- For real-word KG, such as FB15k, we find $M \geq 13365$ , where $|V| = 14951$ .
- Remember, this is for arbitrary OR queries.

Since we cannot embed AND-OR queries in low-dimensional space, can we still handle them?

Ket idea: take all unions out and only do union at the last step!

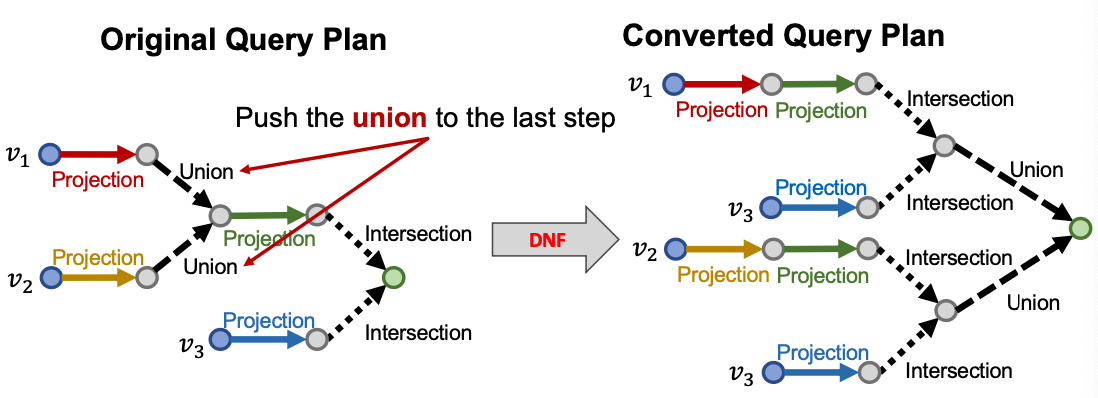
Disjunctive Normal Form

Any AND-OR query can be transformed into equivalent DNF, i.e., disjunction of conjunctive queries.

Given any AND-OR query $q$ ,

q = q_1 \lor q_2 \lor \cdots \lor q_m

where $q_i$ is a conjunctive query.

Now we can first embed each $q_i$ and then “aggregate” at the last step!

Distance Between $q$ and an Entity

Distance between entity embedding and a DNF $q = q_1 \lor q_2 \lor \cdots \lor q_m$ is defined as: /mat\

d_{box} (q,v) = min (d_{box}(q_1,v),\cdots,d_{box}(q_m,v))

Intuition:
- As long as $v$ is the answer to one conjunctive query $q_i$ , then $v$ should be the answer to $q$
- As long aas $v$ is close to one conjunctive query $q_i$ , then $v$ should be close to $q$ in the embedding space.
- The process of embedding any AND-OR query $q$
  1. Transform $q$ to equivalent DNF $q_1 \lor \cdots \lor q_m$
  1. Embed $q_1$ to $q_m$
  1. Calculate the (box) distance $d_{box}(q_i,v)$
  1. Take the minimum of all distance
  1. The final score $f_q(v) = -d_{box}(q,v)$

How to train Query2box

Training Overview

Overview and Intuition: (similar to KG completion)
- Given a query embedding $q$ , maximize the score $f_q(v)$ for answers $v \in [q]$ and minimize the score $f_q(v')$ for negative answers $v' \notin [q]$

Trainable parameter:
- Entity embeddings with $d|V|$ # params
- Relation embeddings with $2d|R|$ # params
- Intersection operator

How to achieve a query, its answer, its negative answers from the KG to train the parameters?

How to split the KG for query answering

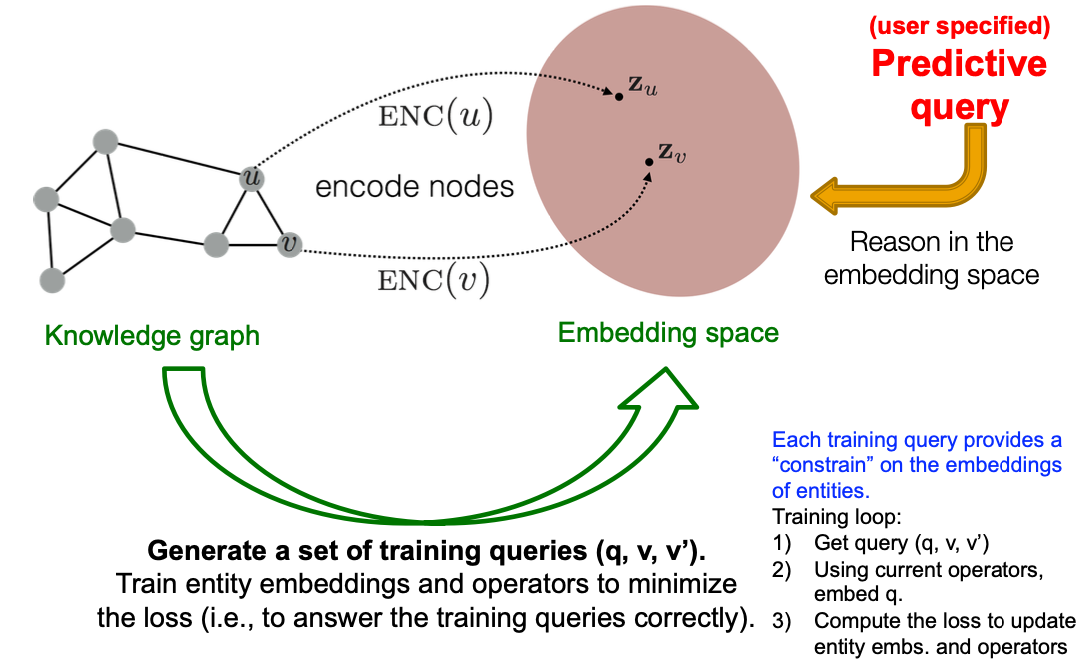
Training: Details

Training:
1. Sample a query $q$ from the training graph $G_{train}$ , answer $v \in [q]_{G_{train}}$ , and non-answer $v' \notin [q]_{G_{train}}$
1. Embed the query $q$
  - Use current operators, to compute query embedding.
1. Calculate the score $f_q(v)$ and $f_q(v')$
1. Optimize embeddings and operations to minimize the loss $\mathcal{l}$ (maximize $f_q(v)$ while minimize $f_q(v')$ ):
$l = - \log \sigma(f_q(v)) - \log (1- \sigma (f_q(v')))$

Query Generation from Templates

Generate queries from multiple query templates:

How can we generate a complex query?

We start with a query template

Query template is an abstraction of the query

We generate a query by instantiating every variable with a concrete entity and relation from the KG
- E.g., instantiate Anchor1 with ESR2 (a node on KG)
- E.g., instantiate Rel1 with Assoc (an edge on KG)

How to instantiate query template given a KG?

How to instantiate a query template given a KG?

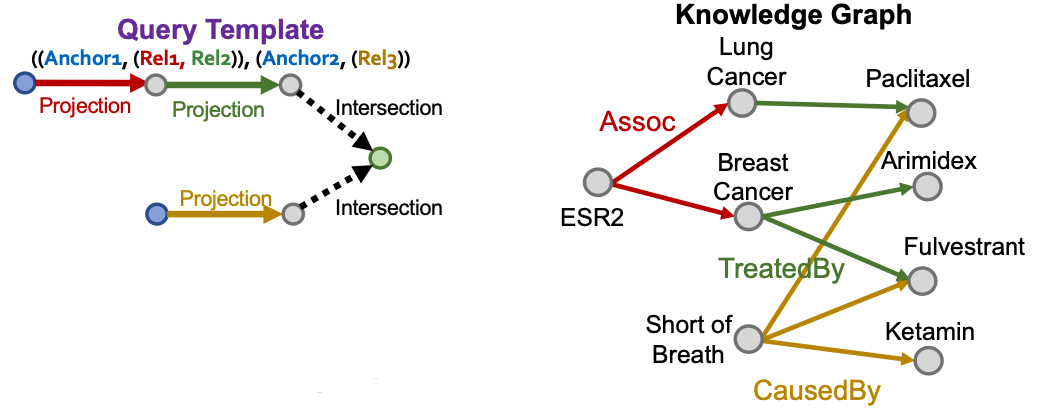
Overview: Start from instantiating the answer node of the query template and then iteratively instantiate the other edges and nodes until we ground all the anchor nodes.

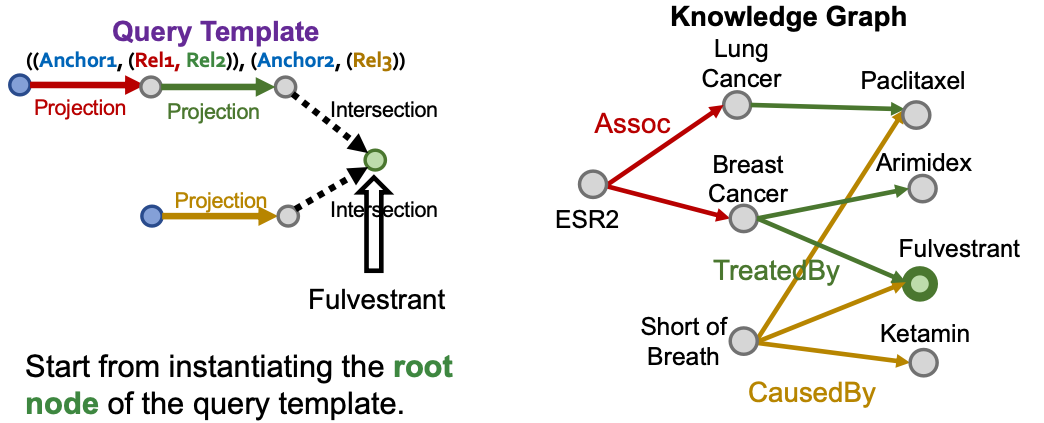
Randomly pick one entity from KG as the root node, e.g., we pick Fulvestrant

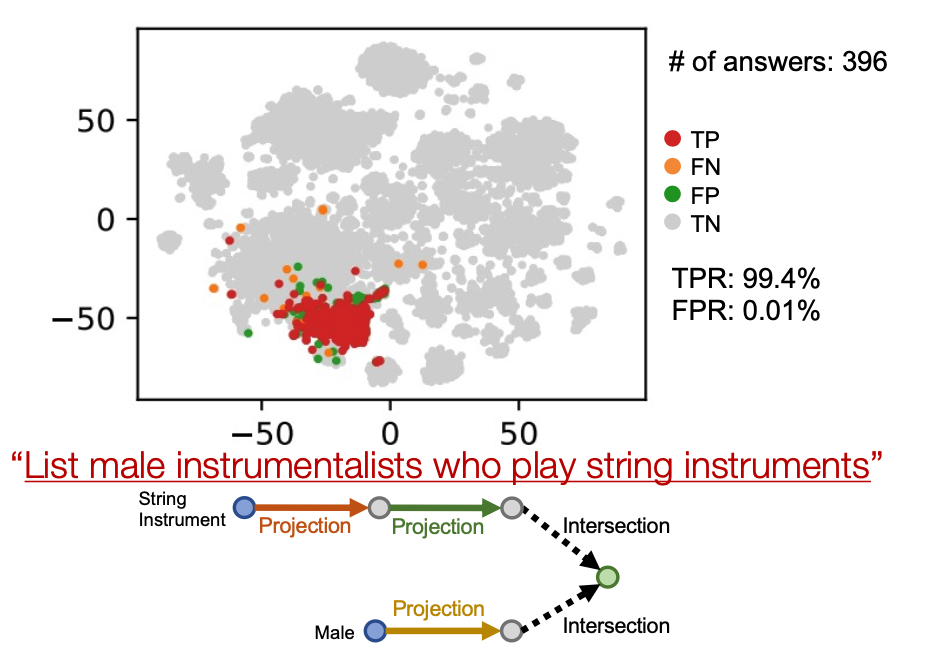
Now we look at intersection. What we have is that the intersection of the sets of entities is Fulvestrant, then naturally the two should also contain Fulvestrant.

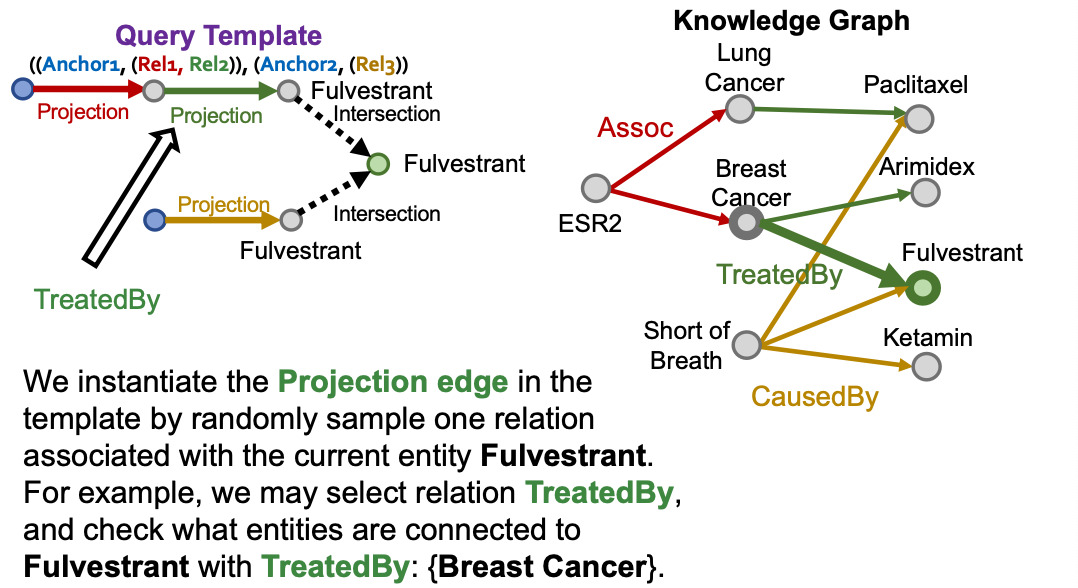
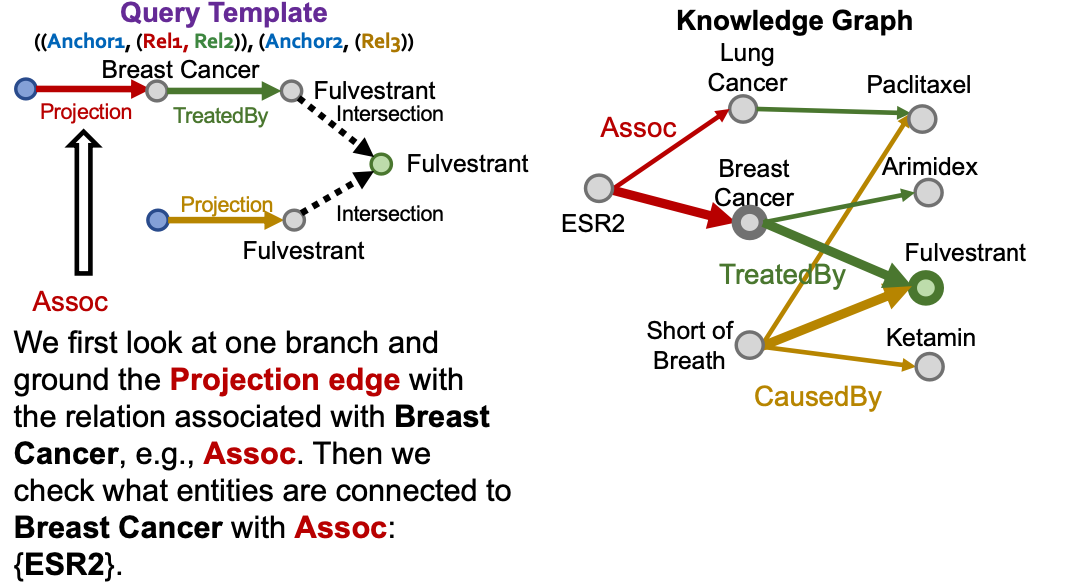
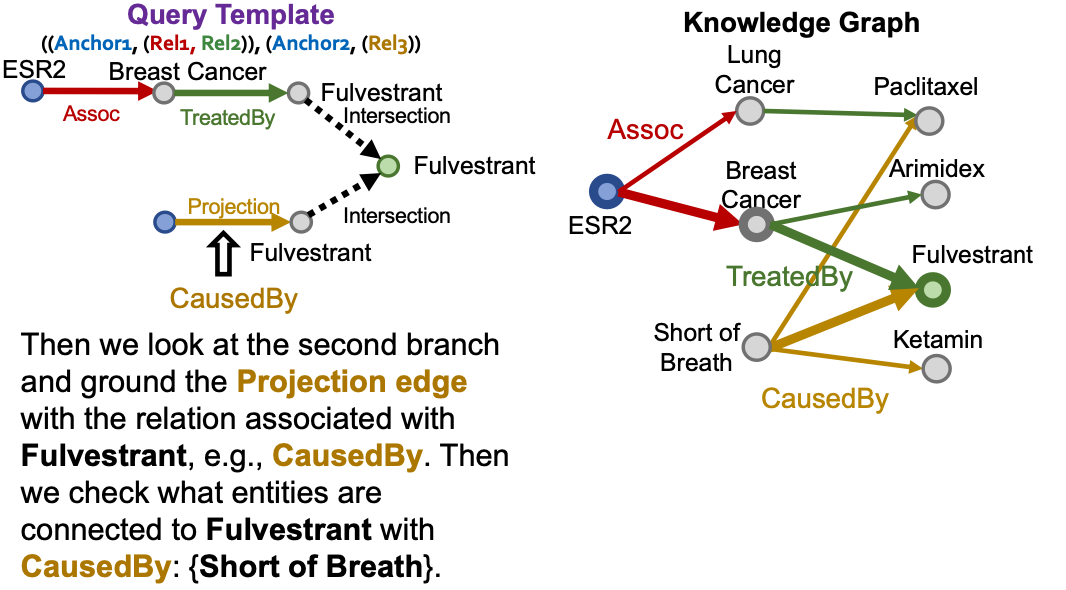
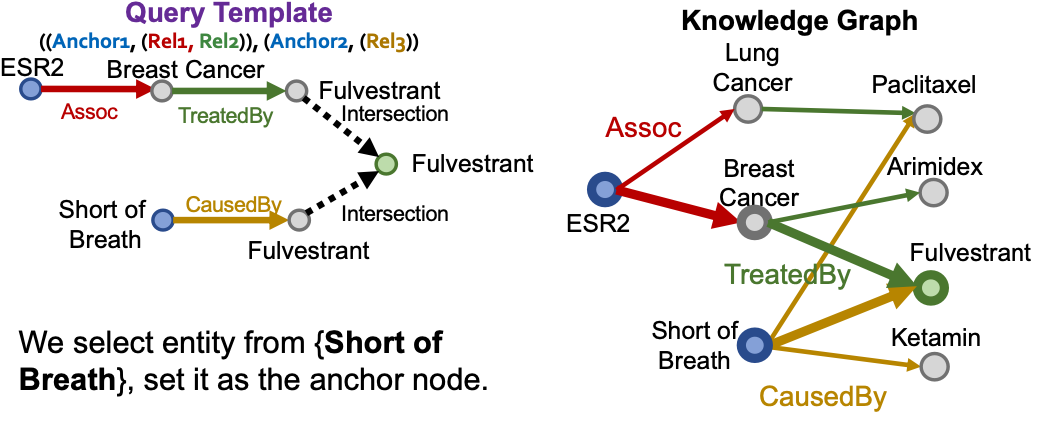
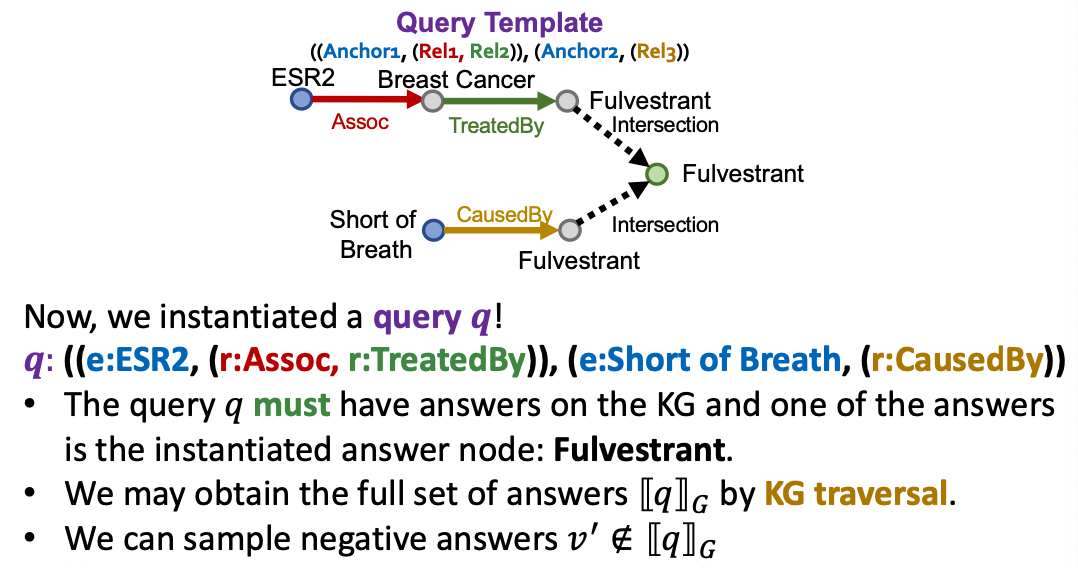
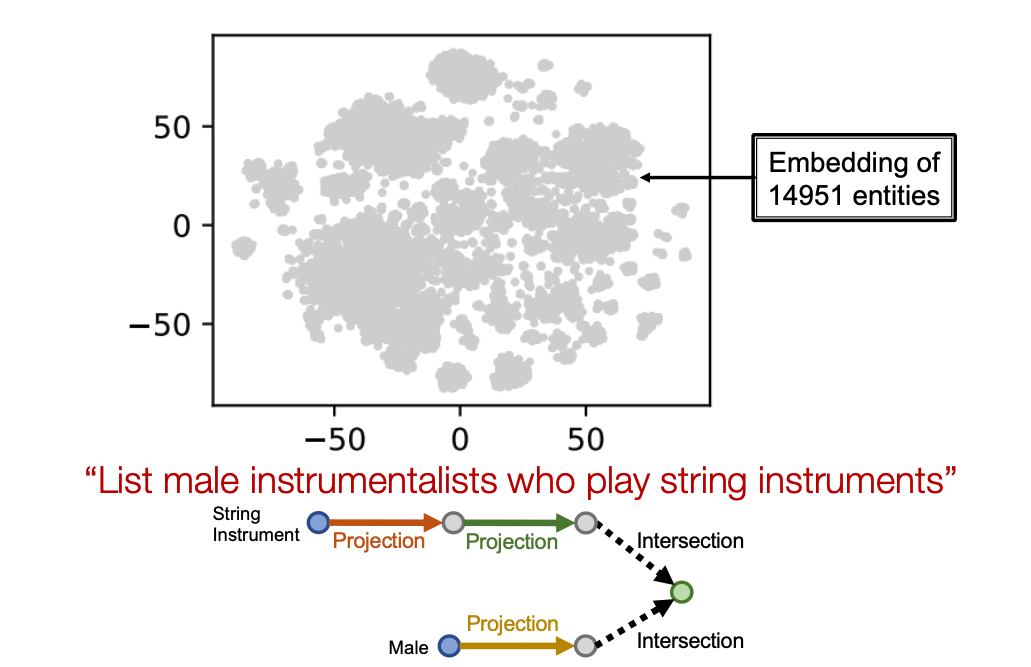
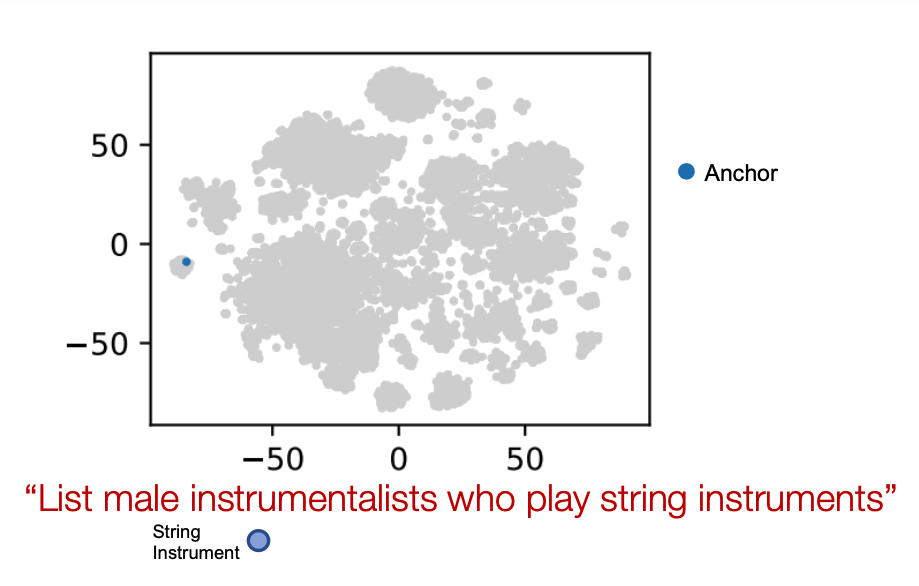
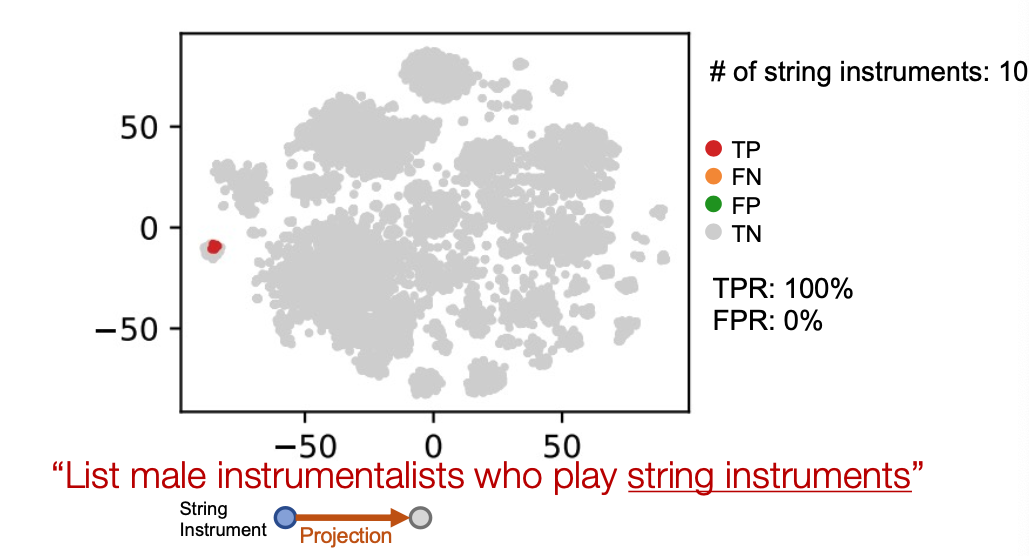
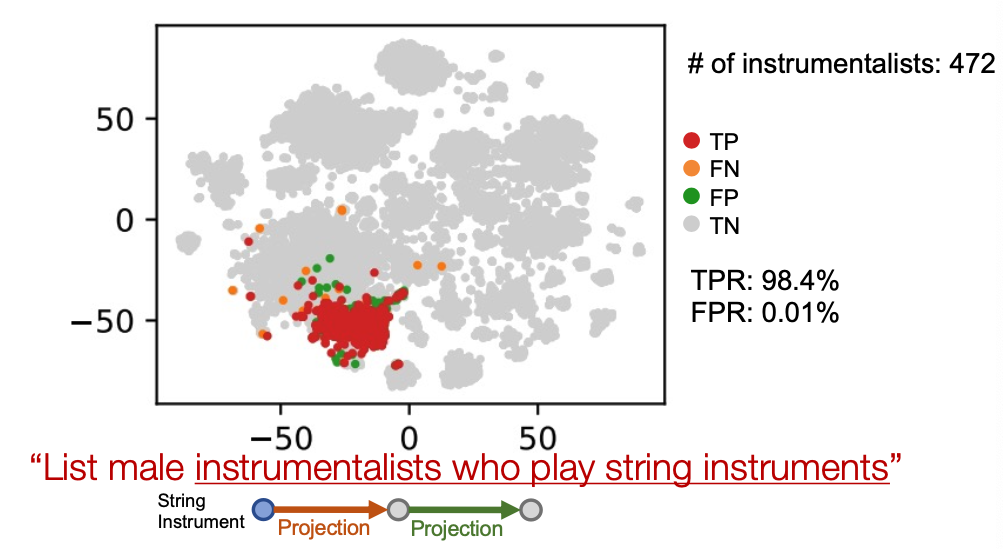
Example of Query2box

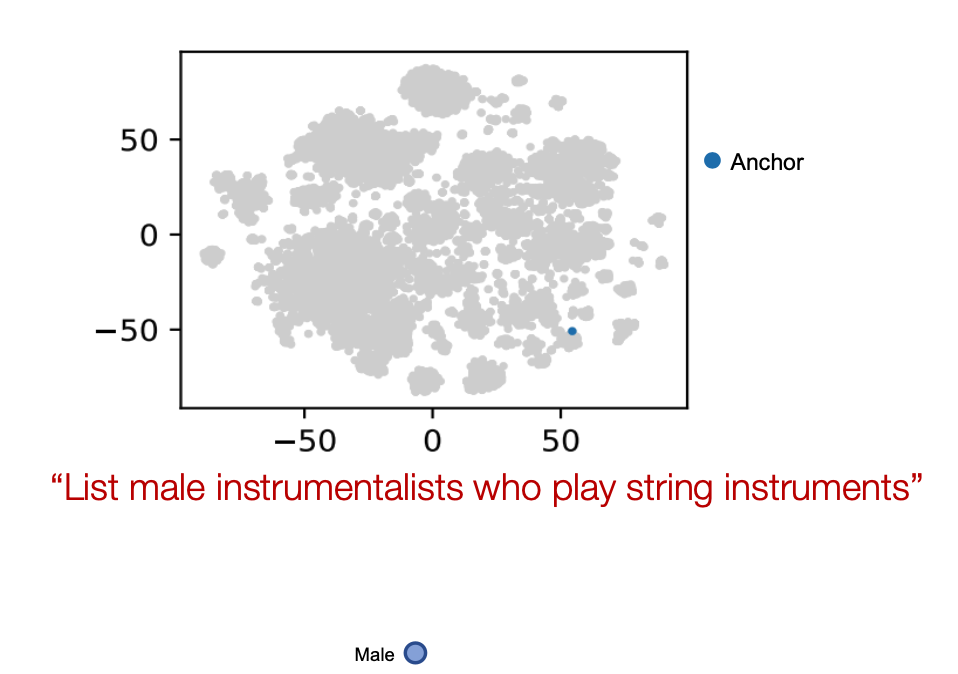
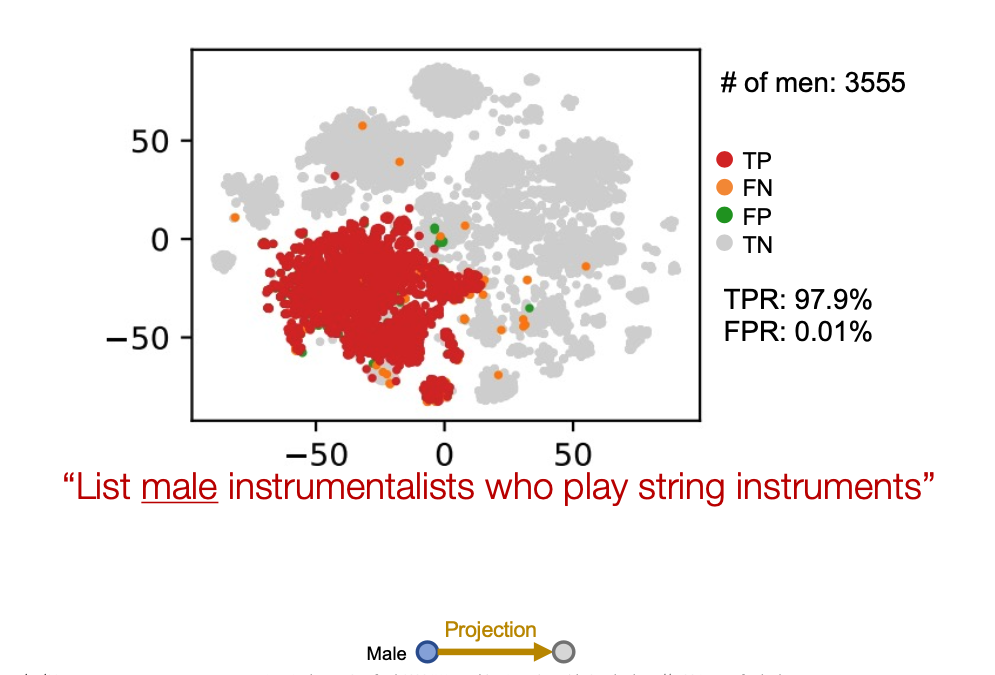
Example: “List male instrumentalists who play string instruments”